|
–§–æ—Ä—É–º –Ý–∞–¥–∏–æ–ö–æ—Ç • –ü—Ä–æ—Å–º–æ—Ç—Ä —Ç–µ–º—ã - –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã
–°–æ–æ–±—â–µ–Ω–∏—è –±–µ–∑ –æ—Ç–≤–µ—Ç–æ–≤ | –ê–∫—Ç–∏–≤–Ω—ã–µ —Ç–µ–º—ã
 
|
–°—Ç—Ä–∞–Ω–∏—Ü–∞ 1 –∏–∑ 1
|
[ –°–æ–æ–±—â–µ–Ω–∏–π: 10 ] |
|
| –ê–≤—Ç–æ—Ä |
–°–æ–æ–±—â–µ–Ω–∏–µ |
Vendein_RaZoR

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –Ω–æ—è 17, 2013 21:09:25 |
|
| –°–≤–µ—Ä–ª–∏—Ç —Ç–µ–∫—Å—Ç–æ–ª–∏—Ç –∫–æ–≥—Ç—è–º–∏ |
–ö–∞—Ä–º–∞: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: -1
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä –∏—é–Ω 22, 2011 21:14:17
–°–æ–æ–±—â–µ–Ω–∏–π: 1158
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–í –æ–±—â–µ–º —Å–æ–±—Å–Ω–æ –ø–æ —Å–∞–±–∂—É , –Ω—É–∂–Ω–æ –Ω–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã –∫–æ–Ω—Å—Ç—Ä—É–∫—Ü–∏–∏ —Å –∂–∏–ª–æ–π –ø–æ —Å–µ—Ä–µ–¥–∏–Ω–µ —Å —Ç–æ–∫–æ–º –∏ —Ü–∏–ª–∏–Ω–¥—Ä–æ–º —Å–Ω–∞—Ä—É–∂–∏ —Ç–æ–∂–µ —Å —Ç–æ–∫–æ–º (—Ç–µ–∫—É—Ç –≤ —Ä–∞–∑–Ω—ã—Ö –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏—è—Ö) , –º–µ–∂–¥—É –Ω–∏–º–∏ –ø–∞—Ä–∞–º–∞–≥–Ω–µ—Ç–∏–∫. –ò —Å–¥–µ–ª–∞—Ç—å —ç—Ç–æ –º–æ–∂–Ω–æ 2 —Å–ø–æ—Å–æ–±–∞–º–∏ –∫–∞–∫ –ø–æ–∫–∞–∑–∞–Ω–æ –Ω–∞ —Ä–∏—Å—É–Ω–∫–µ . –í –¥–∞–Ω–Ω–æ–º —Å–ª—É—á–∞–µ –æ—Ç–≤–µ—Ç—ã –ø–æ–ª—É—á–∞—é—Ç—Å—è –æ–¥–∏–Ω–∞–∫–æ–≤—ã–º–∏ . –°–æ–±—Å–Ω–æ –ø–æ—á–µ–º—É —Ç–∞–∫ –ø—Ä–æ–∏—Å—Ö–æ–¥–∏—Ç , –∫–∞–∫–æ–π –∫–æ–Ω—Ç—É—Ä –∑–∞–º–∫–Ω—É—Ç—ã–π –º—ã –±–µ—Ä–µ–º –≤ —Å–ª—É—á–∞–µ —Å –§ = LI ?  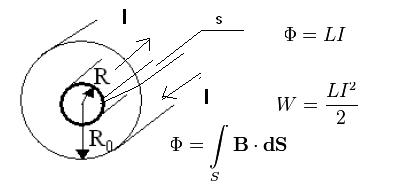 –ó–´ —Ç—É —Ç–µ–º—É –º–æ–∂–Ω–æ —É–¥–∞–ª—è—Ç—å .
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
a_skr

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –Ω–æ—è 17, 2013 21:18:55 |
|
| –í—ã–º–æ–≥–∞—Ç–µ–ª—å –ø—Ä–∏–ø–æ—è |
–ö–∞—Ä–º–∞: 22
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 114
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –∏—é–Ω 14, 2010 13:07:29
–°–æ–æ–±—â–µ–Ω–∏–π: 630
–û—Ç–∫—É–¥–∞: –ñ—É–∫–æ–≤—Å–∫–∏–π
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–í—ã —Ö–æ—Ç–∏—Ç–µ —Å–ø—Ä–æ—Å–∏—Ç—å, –∫–∞–∫ —Ç–æ–∫ I –≤–ª–∏—è–µ—Ç –Ω–∞ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å? –ò –≤–ª–∏—è–µ—Ç-–ª–∏?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
Vendein_RaZoR

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –Ω–æ—è 17, 2013 21:21:00 |
|
| –°–≤–µ—Ä–ª–∏—Ç —Ç–µ–∫—Å—Ç–æ–ª–∏—Ç –∫–æ–≥—Ç—è–º–∏ |
–ö–∞—Ä–º–∞: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: -1
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä –∏—é–Ω 22, 2011 21:14:17
–°–æ–æ–±—â–µ–Ω–∏–π: 1158
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–ù–µ—Ç —è —Ö–æ—á—É —Å–ø—Ä–æ—Å–∏—Ç—å –∫–∞–∫ –ø–æ–ª—É—á–∞—é—Ç—Å—è —Ä–∞–≤–Ω—ã –æ—Ç–≤–µ—Ç—ã –ø—Ä–∏ —Ä–∞–∑–Ω–æ–º —Å–ø–æ—Å–æ–±–µ –Ω–∞—Ö–æ–∂–¥–µ–Ω–∏—è –≤–µ–ª–∏—á–∏–Ω—ã –∏ –≥–¥–µ –ø–æ —Å–∞–º–æ–π –ø–µ—Ä–≤–æ–π —Ñ–æ—Ä–º—É–ª–µ —É –Ω–∞—Å –ø–æ–ª—É—á–∞–µ—Ç—Å—è –∑–∞–º–∫–Ω—É—Ç—ã–π –∫–æ–Ω—Ç—É—Ä —Å —Ç–æ–∫–æ–º ?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
a_skr

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –Ω–æ—è 17, 2013 21:37:05 |
|
| –í—ã–º–æ–≥–∞—Ç–µ–ª—å –ø—Ä–∏–ø–æ—è |
–ö–∞—Ä–º–∞: 22
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 114
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –∏—é–Ω 14, 2010 13:07:29
–°–æ–æ–±—â–µ–Ω–∏–π: 630
–û—Ç–∫—É–¥–∞: –ñ—É–∫–æ–≤—Å–∫–∏–π
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–°–ø—Ä–æ—à—É –µ—â–µ —Ä–∞–∑: –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –∫–æ–Ω—Å—Ç—Ä—É–∫—Ü–∏–∏ –ö–ê–ö –∑–∞–≤–∏—Å–∏—Ç –æ—Ç –ø—Ä–æ—Ü–µ—Å—Å–æ–≤ –≤–Ω—É—Ç—Ä–∏ –∫–æ–Ω—Å—Ç—Ä—É–∫—Ü–∏–∏ (–Ω–∞–ø—Ä–∏–º–µ—Ä, —Ç–æ–∫–∞, –ø—Ä–æ—Ö–æ–¥—è—â–µ–≥–æ –≤ –µ–≥–æ —á–∞—Å—Ç—è—Ö)?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
Vendein_RaZoR

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –Ω–æ—è 17, 2013 23:53:46 |
|
| –°–≤–µ—Ä–ª–∏—Ç —Ç–µ–∫—Å—Ç–æ–ª–∏—Ç –∫–æ–≥—Ç—è–º–∏ |
–ö–∞—Ä–º–∞: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: -1
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä –∏—é–Ω 22, 2011 21:14:17
–°–æ–æ–±—â–µ–Ω–∏–π: 1158
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–ù–µ –ø–æ–Ω—è–ª —á—Ç–æ –∑–Ω–∞—á–∏—Ç –∫–∞–∫ –∑–∞–≤–∏—Å–∏—Ç ? –í—ã—Ä–∞–∂–∞–π—Ç–µ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å , —Ç–æ–∫ —Å—á–∏—Ç–∞—Ç—å –ø–æ—Å—Ç–æ—è–Ω–Ω—ã–º , —Ç–æ–ª—å–∫–æ –º–∞–≥–Ω–∏—Ç–Ω–∞—è –ø—Ä–æ–Ω–∏—Ü–∞–µ–º–æ—Å—Ç—å –æ—Ç —Ä–∞–¥–∏—É—Å–∞ –º–µ–∂–¥—É –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–∞–º–∏ –∑–∞–≤–∏—Å–∏—Ç –∏ –≤—Å—ë 
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
a_skr

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω –Ω–æ—è 18, 2013 11:35:13 |
|
| –í—ã–º–æ–≥–∞—Ç–µ–ª—å –ø—Ä–∏–ø–æ—è |
–ö–∞—Ä–º–∞: 22
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 114
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –∏—é–Ω 14, 2010 13:07:29
–°–æ–æ–±—â–µ–Ω–∏–π: 630
–û—Ç–∫—É–¥–∞: –ñ—É–∫–æ–≤—Å–∫–∏–π
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–¶–∏—Ç–∞—Ç–∞: –°–≤–æ–π—Å—Ç–≤–∞ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç–∏:
...
–ò–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –∑–∞–≤–∏—Å–∏—Ç —Ç–æ–ª—å–∫–æ –æ—Ç –≥–µ–æ–º–µ—Ç—Ä–∏—á–µ—Å–∫–∏—Ö —Ä–∞–∑–º–µ—Ä–æ–≤ –∫–æ–Ω—Ç—É—Ä–∞ –∏ –º–∞–≥–Ω–∏—Ç–Ω—ã—Ö —Å–≤–æ–π—Å—Ç–≤ —Å—Ä–µ–¥—ã
–ï—Å–ª–∏ —Å—á–∏—Ç–∞—Ç—å —Å—Ç—Ä—É–∫—Ç—É—Ä—É —Ç–æ–∫–æ–≤ (—Ç–æ—á–Ω–æ –∏–ª–∏ –ø—Ä–∏–±–ª–∏–∂–µ–Ω–Ω–æ) —Ñ–∏–∫—Å–∏—Ä–æ–≤–∞–Ω–Ω–æ–π, —Ç–æ –µ—Å—Ç—å –µ—Å–ª–∏ —Ç–æ–∫–∏ –Ω–µ –ø–µ—Ä–µ—Ä–∞—Å–ø—Ä–µ–¥–µ–ª—è—é—Ç—Å—è –ø–æ –æ–±—ä–µ–º—É –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–∞ –≤ –ø—Ä–æ—Ü–µ—Å—Å–µ –∏—Ö –≤–æ–∑–±—É–∂–¥–µ–Ω–∏—è.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
Vendein_RaZoR

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω –Ω–æ—è 18, 2013 19:42:50 |
|
| –°–≤–µ—Ä–ª–∏—Ç —Ç–µ–∫—Å—Ç–æ–ª–∏—Ç –∫–æ–≥—Ç—è–º–∏ |
–ö–∞—Ä–º–∞: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: -1
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä –∏—é–Ω 22, 2011 21:14:17
–°–æ–æ–±—â–µ–Ω–∏–π: 1158
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–ù—É —Ö–æ—Ä–æ—à–æ , –≤–æ—Ç –¥–æ–ø—É—Å—Ç–∏–º —è —Ç–∞–∫–æ–π –ø—Ä–∏–º–µ—Ä –Ω–∞—à–µ–ª , –∫–æ–≥–¥–∞ –º—ã —Å—á–∏—Ç–∞–µ–º –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–æ –º–µ–∂–¥—É —Ü–∏–ª–∏–Ω–¥—Ä–∏—á–µ—Å–∫–∏–º–∏ –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–∞–º–∏ –∫–∞–∫ –Ω–∞ –∫–∞—Ä—Ç–∏–Ω–∫–µ –≤—ã—à–µ —Å –º–∞–≥–Ω–∏—Ç–Ω–æ–π –ø—Ä–æ–Ω–∏—Ü–∞–µ–º–æ—Å—Ç—å—é = 1 –∏ –≤—ã—á–∏—Å–ª—è–µ–º –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –æ–ø—è—Ç—å –∂–µ –¥–≤—É–º—è —Å–ø–æ—Å–æ–±–∞–º–∏ –∫–∞–∫ –±—ã–ª–æ —Å–∫–∞–∑–∞–Ω–æ , —Ç–æ —Ä–µ–∑—É–ª—å—Ç–∞—Ç—ã –æ—Ç–ª–∏—á–∞—é—Ç—Å—è , –Ω–æ –Ω–µ —Å–∏–ª—å–Ω–æ , –ø–æ –º–µ—Ä–µ —É–º–µ–Ω—å—à–µ–Ω–∏—è –¥–∏–∞–º–µ—Ç—Ä–∞ —Ü–µ–Ω—Ç—Ä–∞–ª—å–Ω–æ–≥–æ –ø—Ä–æ–≤–æ–¥–∞ —Ä–µ–∑—É–ª—å—Ç–∞—Ç—ã –ø–æ—Å—Ç–µ–ø–µ–Ω–Ω–æ –Ω–∞—á–∏—Ç–∞—é—Ç –≤—ã—Ä–∞–≤–Ω–∏–≤–∞—Ç—å—Å—è . –ö–∞–∫ –æ–±—ä—è—Å–Ω–∏—Ç—å —Ç–∞–∫–æ–µ ? 
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
Alex-lab

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°—Ä –Ω–æ—è 20, 2013 14:10:00 |
|
| –ü–æ—Ç—Ä–æ–≥–∞–ª –ª–∞–ø–æ–π –ø–∞—è–ª—å–Ω–∏–∫ |
 |
–ö–∞—Ä–º–∞: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 54
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä –Ω–æ—è 20, 2013 11:29:26
–°–æ–æ–±—â–µ–Ω–∏–π: 308
–û—Ç–∫—É–¥–∞: –ú–∞–Ω—á–µ—Å—Ç–µ—Ä
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–î–∞–≤–∞–π—Ç–µ –ø–æ –ø–æ—Ä—è–¥–∫—É. –û–ø–∏—à–∏—Ç–µ –ø–æ–∂–∞–ª—É–π—Å—Ç–∞ –º–µ—Ç–æ–¥ –Ω–∞—Ö–æ–∂–¥–µ–Ω–∏—è ‚Ññ1 –∏ –º–µ—Ç–æ–¥ ‚Ññ2.
–ï—Å–ª–∏ —è –ø—Ä–∞–≤–∏–ª—å–Ω–æ –ø–æ–Ω—è–ª, –ø–µ—Ä–≤—ã–π —á–µ—Ä–µ–∑ –ø–æ—Ç–æ–∫, –≤—Ç–æ—Ä–æ–π —á–µ—Ä–µ–∑ —ç–Ω–µ—Ä–≥–∏—é –ø–æ–ª—è? –ò–ª–∏ –í—ã –∏–º–µ–ª–∏ –≤–≤–∏–¥—É —á—Ç–æ-—Ç–æ –¥—Ä—É–≥–æ–µ?
_________________
–ü—Ä–∏ —Ä–µ—à–µ–Ω–∏–µ –Ω–∞–∏–±–æ–ª–µ–µ —Å–ª–æ–∂–Ω—ã—Ö –∑–∞–¥–∞—á, –±–æ–ª—å—à–∏–Ω—Å—Ç–≤–æ, –∫–∞–∫ –ø—Ä–∞–≤–∏–ª–æ, –æ—à–∏–±–∞–µ—Ç—Å—è...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
rustot

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç –Ω–æ—è 21, 2013 15:10:46 |
|
| –ü–æ—Å—Ç–∞–≤—â–∏–∫ –≤–∞–ª–µ—Ä—å—è–Ω–∫–∏ –¥–ª—è –ö–æ—Ç–∞ |
–ö–∞—Ä–º–∞: 5
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 61
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü—Ç –æ–∫—Ç 23, 2009 15:32:35
–°–æ–æ–±—â–µ–Ω–∏–π: 1929
–û—Ç–∫—É–¥–∞: –ß–µ–ª—è–±–∏–Ω—Å–∫
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
—Ñ–æ—Ä–º—É–ª–∞ —Å –ø–æ—Ç–æ–∫–æ–º, –ø–µ—Ä–µ—Å–µ–∫–∞—é—â–∏–º –∑–∞–º–∫–Ω—É—Ç—ã–π –∫–æ–Ω—Ç—É—Ä - –ø—Ä–æ—Å—Ç–æ —Ñ–æ—Ä–º—É–ª–∞ –¥–ª—è —á–∞—Å—Ç–Ω–æ–≥–æ —Å–ª—É—á–∞—è, –∞ –Ω–µ –∫–∞–∫–æ–π-—Ç–æ —É–Ω–∏–≤–µ—Ä—Å–∞–ª—å–Ω—ã–π –ø—Ä–∏–Ω—Ü–∏–ø. –ø—Ä—è–º–æ–π –±–µ—Å–∫–æ–Ω–µ—á–Ω—ã–π –ø—Ä–æ–≤–æ–¥ —Ç–∞–∫–∂–µ –∏–º–µ–µ—Ç –ø–æ–≥–æ–Ω–Ω—É—é –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å, –∑–∞–≤–∏—Å—è—â—É—é —Ç–æ–ª—å–∫–æ –æ—Ç –µ–≥–æ –¥–∏–∞–º–µ—Ç—Ä–∞, —á—Ç–æ –Ω–∏ –≤ –∫–∞–∫–∏–µ —Ñ–æ—Ä–º—É–ª—ã —Å –ø–ª–æ—â–∞–¥—è–º–∏ –∑–∞–≤–µ–¥–æ–º–æ –Ω–µ –≤–ø–∏—Å—ã–≤–∞–µ—Ç—Å—è.
—Ä–µ–∞–ª—å–Ω–æ —á—Ç–æ–±—ã –Ω–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω—É–∂–Ω–æ —Ä–∞–∑–±–∏—Ç—å –≤–µ—Å—å –ø—Ä–æ–≤–æ–¥–Ω–∏–∫ –Ω–∞ "—Ç–æ—á–∫–∏" —Å —Ç–æ–∫–æ–º (–≤ —Å–∏–º–º–µ—Ç—Ä–∏—á–Ω—ã—Ö —Å–ª—É—á–∞—è—Ö –Ω–∞ "–Ω–∏—Ç–∏" —Å —Ç–æ–∫–æ–º) –∏ –ø–æ—Å—á–∏—Ç–∞—Ç—å –∫–∞–∫–æ–µ –≤–∏—Ö—Ä–µ–≤–æ–µ –ø–æ–ª–µ E —Å–æ–∑–¥–∞–µ—Ç –∏–∑–º–µ–Ω–µ–Ω–∏–µ –ø–ª–æ—Ç–Ω–æ—Å—Ç–∏ —Ç–æ–∫–∞ j –≤ –∫–∞–∂–¥–æ–π –∏–∑ —Ç–æ—á–µ–∫/–Ω–∏—Ç–µ–π –≤ –¥—Ä—É–≥–∏—Ö —Ç–æ—á–∫–∞—Ö/–Ω–∏—Ç—è—Ö. —á–∏—Å–ª–µ–Ω–Ω–æ –Ω–∞ –∫–æ–º–ø–µ —Ä–µ—à–∞–µ—Ç—Å—è –≤—Å–µ–≥–¥–∞. –∞–Ω–∞–ª–∏—Ç–∏—á–µ—Å–∫–∏ —Ç–æ—á–Ω–æ –ø—Ä–∞–∫—Ç–∏—á–µ—Å–∫–∏ –Ω–∏–∫–æ–≥–¥–∞, –≤—Å–µ –∞–Ω–∞–ª–∏—Ç–∏—á–µ—Å–∫–∏–µ —Ñ–æ—Ä–º—É–ª—ã –ø—Ä–∏–±–ª–∏–∂–µ–Ω–Ω—ã–µ
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
Alex-lab

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –Ω–∞ –µ–¥–∏–Ω–∏—Ü—É –¥–ª–∏–Ω—ã  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç –Ω–æ—è 21, 2013 16:25:20 |
|
| –ü–æ—Ç—Ä–æ–≥–∞–ª –ª–∞–ø–æ–π –ø–∞—è–ª—å–Ω–∏–∫ |
 |
–ö–∞—Ä–º–∞: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 54
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä –Ω–æ—è 20, 2013 11:29:26
–°–æ–æ–±—â–µ–Ω–∏–π: 308
–û—Ç–∫—É–¥–∞: –ú–∞–Ω—á–µ—Å—Ç–µ—Ä
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–î–ª—è —Ä–µ—à–µ–Ω–∏—è –∑–∞–¥–∞—á–∏ –Ω—É–∂–Ω–æ —É–º–µ—Ç—å –Ω–∞—Ö–æ–¥–∏—Ç—å –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å —Ç–æ–Ω–∫–æ–≥–æ –±–ª–∏–Ω–∞ –Ω–∞—Ä–µ–∑–∞–Ω–Ω–æ–≥–æ –∏–∑ —Ç–∞–∫–æ–≥–æ –ø—Ä–æ–≤–æ–¥–∞, –∞ –∑–∞—Ç–µ–º –∏–Ω—Ç–µ–≥—Ä–∏—Ä–æ–≤–∞—Ç—å –æ—Ç 0 –¥–æ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç–∏ –ø–æ –¥–ª–∏–Ω–µ –∫–∞–±–µ–ª—è (–¥–∞ –ø—Ä–æ—Å—Ç—è—Ç –º–µ–Ω—è –∫–æ—Ç—ã  ). –ò–Ω—Ç–µ–≥—Ä–∞–ª –¥–æ–ª–∂–µ–Ω –ø–æ–ª—É—á–∏—Ç—å—Å—è —Å—Ö–æ–¥—è—â–∏–º—Å—è. –ë–ª–∏–Ω –¥–æ–ª–∂–µ–Ω –±—ã—Ç—å –∑–∞–≥–ª—É—à–µ–Ω —Å –æ–±–µ–∏—Ö —Å—Ç–æ—Ä–æ–Ω –∫–æ—Ä–æ—Ç–∫–æ–∑–∞–º–∫–Ω—É—Ç–Ω—ã–º–∏ –¥–∏—Å–∫–∞–º–∏. –ü–æ—Ç–æ–º –ø—Ä–∏ —Å—É–º–º–∏—Ä–æ–≤–∞–Ω–∏–∏ –æ–Ω–∏ —Å–æ–∫—Ä–∞—Ç—è—Ç—Å—è. –ò–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –±–ª–∏–Ω–∞ –Ω–∞—Ö–æ–¥–∏—Ç—Å—è —Å –ø–æ–º–æ—â—å—é —Ç–µ–æ—Ä–µ–º—ã –ì–∞—É—Å—Å–∞ –¥–ª—è –º–∞–≥–Ω–∏—Ç–Ω–æ–≥–æ –ø–æ–ª—è. –ï—Å–ª–∏ —Ç–æ–∫ –≤ –∫–æ–Ω—Ç—É—Ä–µ –∏–∑–≤–µ—Å—Ç–µ–Ω, –ª–µ–≥–∫–æ –Ω–∞–π—Ç–∏ –Ω–∞–ø—Ä—è–∂–µ–Ω–Ω–æ—Å—Ç—å –ø–æ–ª—è, –∞ –∏–∑ –Ω–µ–µ, –∑–Ω–∞—è –≤–æ—Å–ø—Ä–∏–∏–º—á–∏–≤–æ—Å—Ç—å –∏–ª–∏ –ø—Ä–æ–Ω–∏—Ü–∞–µ–º–æ—Å—Ç—å, –º–∞–≥–Ω–∏—Ç–Ω—É—é –∏–Ω–¥—É–∫—Ü–∏—é. –ù—É –∞ –∏–∑ –∏–Ω–¥—É–∫—Ü–∏–∏ –Ω–∞–π—Ç–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å. –ù–æ –≤–æ–ø—Ä–æ—Å —Ç–æ –Ω–µ –≤ —Ä–µ—à–µ–Ω–∏–∏ –∑–∞–¥–∞—á–∏, –∞ –≤ —á—ë–º-—Ç–æ –¥—Ä—É–≥–æ–º? –ê–≤—Ç–æ—Ä –∂–µ –Ω–µ —Ä–µ—à–µ–Ω–∏–µ —Å–ø—Ä–∞—à–∏–≤–∞–ª. 
_________________
–ü—Ä–∏ —Ä–µ—à–µ–Ω–∏–µ –Ω–∞–∏–±–æ–ª–µ–µ —Å–ª–æ–∂–Ω—ã—Ö –∑–∞–¥–∞—á, –±–æ–ª—å—à–∏–Ω—Å—Ç–≤–æ, –∫–∞–∫ –ø—Ä–∞–≤–∏–ª–æ, –æ—à–∏–±–∞–µ—Ç—Å—è...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
 
|
–°—Ç—Ä–∞–Ω–∏—Ü–∞ 1 –∏–∑ 1
|
[ –°–æ–æ–±—â–µ–Ω–∏–π: 10 ] |
|
–ö—Ç–æ —Å–µ–π—á–∞—Å –Ω–∞ —Ñ–æ—Ä—É–º–µ |
–°–µ–π—á–∞—Å —ç—Ç–æ—Ç —Ñ–æ—Ä—É–º –ø—Ä–æ—Å–º–∞—Ç—Ä–∏–≤–∞—é—Ç: –Ω–µ—Ç –∑–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω–Ω—ã—Ö –ø–æ–ª—å–∑–æ–≤–∞—Ç–µ–ª–µ–π –∏ –≥–æ—Å—Ç–∏: 38 |
|
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –Ω–∞—á–∏–Ω–∞—Ç—å —Ç–µ–º—ã
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –æ—Ç–≤–µ—á–∞—Ç—å –Ω–∞ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ —Ä–µ–¥–∞–∫—Ç–∏—Ä–æ–≤–∞—Ç—å —Å–≤–æ–∏ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ —É–¥–∞–ª—è—Ç—å —Å–≤–æ–∏ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –¥–æ–±–∞–≤–ª—è—Ç—å –≤–ª–æ–∂–µ–Ω–∏—è
|
|
|























