|
–§–æ—Ä—É–º –Ý–∞–¥–∏–æ–ö–æ—Ç • –ü—Ä–æ—Å–º–æ—Ç—Ä —Ç–µ–º—ã - –°–æ–µ–¥–∏–Ω–µ–Ω–∏–µ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–æ–≤
–°–æ–æ–±—â–µ–Ω–∏—è –±–µ–∑ –æ—Ç–≤–µ—Ç–æ–≤ | –ê–∫—Ç–∏–≤–Ω—ã–µ —Ç–µ–º—ã
 
|
–°—Ç—Ä–∞–Ω–∏—Ü–∞ 8 –∏–∑ 29
|
[ –°–æ–æ–±—â–µ–Ω–∏–π: 564 ] |
... , , , , , , ... |
| –ê–≤—Ç–æ—Ä |
–°–æ–æ–±—â–µ–Ω–∏–µ |
Gudd-Head

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü—Ç –æ–∫—Ç 25, 2013 14:53:21 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 67
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1065
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —Å–µ–Ω 18, 2008 12:27:21
–°–æ–æ–±—â–µ–Ω–∏–π: 19930
–û—Ç–∫—É–¥–∞: –°—Ç–æ–ª–∏—Ü–∞ –ú–∏—Ä–∞ –°–∞–Ω–∫—Ç-–ü–µ—Ç–µ—Ä–±—É—Ä–≥
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ú–µ–¥–∞–ª–∏: 1

|
Стоило отойти — нафлудили уже 5 страниц. Не-не-не. Только я, значит, придумал элегантное описание этой школьной задачки Slabovik писал(а): Вообще-то это школьная задачка:
Имеется два одинаковых идеальных конденсатора емкостью C. Один конденсатор заряжен до напряжения U, второй разряжен (напряжение 0). Конденсаторы соединяют параллельно двумя медными проволочками длиной L диаметром d. Вычислить, на сколько нагреются проволочки... как тема уже закрыта? Нееет  Я тоже хочу пофлудить. Итак, Дано: два конденсатора ёмкостью С1 и С2, заряженные до U1 и U2 соответственно, и резистор R. Найти: количество тепла, выделившееся на резисторе при соединении конденсаторов через него, взять предел при R —> 0. Количество тепла по закону Джоуля — Ленца есть интеграл по времени (в нашем случае от нуля до бесконечности) выделяющейся на резисторе мощности: 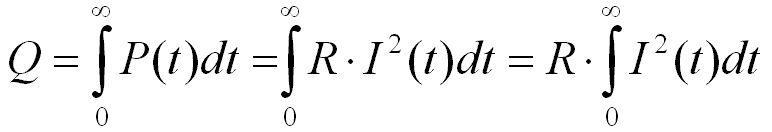 , где закон изменения тока:  Подставляем в интеграл и вычисляем: Спойлер Таким образом, выделенное на резисторе количество тепла не зависит от номинала!!! Это физика. Положив U1 = U, U2 = 0 и C1 = C2 = C, получим искомое С·U²/4. Как видите, оно будет всегда. Но! Если положить R = 0, то в интеграле будет сингулярность. Это математика. Так что говорить о том, куда делась энергия в данной системе без потерь, не имеет физического смысла. Это не идеализация, это грубое нарушение алгебры (деление на ноль). Точно также если замыкать не через резистор, а через идеальную индуктивность L чтобы ограничить бросок тока — будут гармонические незатухающие колебания. И в тот момент, когда на каждом конденсаторе будет по U/2, "недостающая" энергия будет запасена в магнитном поле катушки L·I²/2. Кстати, и про демонический DC-DC преобразователь я тоже подумал, откуда он сделает на двух конденсаторах заряд по 0,707 от первоначального. Эквивалентная схема преобразователя — источник тока, он-то и даст дополнительный заряд 0,41 от первоначального.
_________________
[ –í—Å—ë –¥–µ–ª–æ –Ω–µ —Å—Ç–æ–ª—å–∫–æ –≤ –≤–∞—à–µ–π –≥–ª—É–ø–æ—Å—Ç–∏, —Å–∫–æ–ª—å–∫–æ –≤ –º–æ–µ–π –≥–µ–Ω–∏–∞–ª—å–Ω–æ—Å—Ç–∏ ] [ –ü—Ä–∞–≤–∏–ª—å–Ω–æ –∑–∞–¥–∞–Ω–Ω—ã–π –≤–æ–ø—Ä–æ—Å —Å–æ–¥–µ—Ä–∂–∏—Ç –≤ —Å–µ–±–µ –ø–æ–ª–æ–≤–∏–Ω—É –æ—Ç–≤–µ—Ç–∞ ]
–ò–∑–º–µ—Ä–∏—Ç—å –Ω–Ω–Ω–∞–¥–∞?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
Slabovik

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü—Ç –æ–∫—Ç 25, 2013 19:28:28 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 175
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 7680
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 04, 2013 12:46:59
–°–æ–æ–±—â–µ–Ω–∏–π: 17234
–û—Ç–∫—É–¥–∞: –¢—é–º–µ–Ω—å
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–ë—Ä–∞–≤–æ! –î–æ–±–∞–≤–∏—Ç—å –Ω–µ—á–µ–≥–æ. –Ø –∂–µ —Å —Å–∞–º–æ–≥–æ –Ω–∞—á–∞–ª–∞ —á—É–≤—Å—Ç–≤–æ–≤–∞–ª –ø–æ–¥–≤–æ—Ö –≤ –≤–∞—à–∏—Ö –≤–æ–ø—Ä–æ—Å–∞—Ö. –ê –≤—Å–µ–º –æ—Å—Ç–∞–ª—å–Ω—ã–º —Ö–æ—á—É –æ–±—Ä–∞—Ç–∏—Ç—å –≤–Ω–∏–º–∞–Ω–∏–µ - –≤—Ä–µ–º—è –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç—å. –¢.–µ. –¥–∞–Ω–Ω—ã–π –ø—Ä–æ—Ü–µ—Å—Å –ø–µ—Ä–µ–∑–∞—Ä—è–¥–∞ –≤–æ–æ–±—â–µ –Ω–∏–∫–æ–≥–¥–∞ –Ω–µ –∑–∞–∫–∞–Ω—á–∏–≤–∞–µ—Ç—Å—è –Ω–∏ –ø—Ä–∏ –∫–∞–∫–∏—Ö —É—Å–ª–æ–≤–∏—è—Ö (–∫—Ä–æ–º–µ –∏—Å–∫—Éc—Å—Ç–≤–µ–Ω–Ω–æ –≤–≤–µ–¥—ë–Ω–Ω—ã—Ö –¥–µ–º–æ–Ω–æ–≤ –æ—Ç Gudd-Head, –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –±–ª–∏–∑–∫–æ –∏ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –¥–æ–ª–≥–æ –ø—Ä–∏–±–ª–∏–∂–∞—è—Å—å –∫ –ø—Ä–µ–¥–µ–ª—å–Ω—ã–º (–≤—ã—á–∏—Å–ª–µ–Ω–Ω—ã–º –ø–æ —Ñ–æ—Ä–º—É–ª–µ) –∑–Ω–∞—á–µ–Ω–∏—è–º...
_________________
–û–±—â–µ–Ω–∏–µ–º –Ω–∞ —Ñ–æ—Ä—É–º–µ –ø–æ–¥–ø–∏—Ç—ã–≤–∞—é —Å–≤–æ—é —ç–≥–æ–∏—Å—Ç–∏—á–Ω—É—é, —Å–∫–ª–æ–Ω–Ω—É—é –∫ —Å–∞–º–æ–ª—é–±–æ–≤–∞–Ω–∏—é —Å—É—â–Ω–æ—Å—Ç—å.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
rl55

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 03:35:42 |
|
–ö–∞—Ä–º–∞: 79
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1412
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä —Ñ–µ–≤ 13, 2013 21:59:40
–°–æ–æ–±—â–µ–Ω–∏–π: 16166
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–ö—Ç–æ-—Ç–æ —É–±–µ–∂–¥–∞–ª, —á—Ç–æ –∑–∞–¥–∞—á–∫–∞ –ø—Ä–æ—Å—Ç–∞—è, –Ω–∞ —Å–æ–æ–±—Ä–∞–∑–∏—Ç–µ–ª—å–Ω–æ—Å—å, –∞ —Ç—É—Ç –¥–æ —Å–∏–Ω–≥—É–ª—è—Ä–Ω–æ—Å—Ç–∏ –¥–æ—à–ª–∏. –î–∞–≤–∞–π—Ç–µ –≤—Å–ø–æ–º–Ω–∏–º, —á—Ç–æ —Ö–æ—Ç–µ–ª —É–∑–Ω–∞—Ç—å –¢–° –≤ –∑–∞–¥–∞—á–µ - —ç–Ω–µ—Ä–≥–∏—é —Å–∏—Å—Ç–µ–º—ã –≤ –∫–æ–Ω—Ü–µ –ø—Ä–æ—Ü–µ—Å—Å–∞. –¢.–µ., –ø—Ä–µ–¥–ø–æ–ª–∞–≥–∞–ª–æ—Å—å —Å—Ç–∞—Ü–∏–æ–Ω–∞—Ä–Ω–æ–µ –µ–µ —Å–æ—Å—Ç–æ—è–Ω–∏–µ. –ë–µ—Å–∫–æ–Ω–µ—á–Ω—ã–π –∫–æ–ª–µ–±–∞—Ç–µ–ª—å–Ω—ã–π –ø—Ä–æ—Ü–µ—Å—Å –Ω–µ –ø–æ–∑–≤–æ–ª—è–µ—Ç —ç—Ç–æ —Å–¥–µ–ª–∞—Ç—å. –ò —Ç–æ–ª—å–∫–æ –ø—Ä–æ—Ü–µ—Å—Å —Å –∏–∑–ª—É—á–µ–Ω–∏–µ–º —ç–Ω–µ—Ä–≥–∏–∏ –ø—Ä–∏–≤–æ–¥–∏—Ç –∫ –≤—ã–≤–æ–¥—É, –≤—ã—á–∏—Å–ª–µ–Ω–Ω–æ–º—É –¢–°. –ü—Ä–∞–≤–¥–∞ –∏ –∑–¥–µ—Å—å –µ—Å—Ç—å –∑–∞–≥–≤–æ–∑–¥–∫–∞ - –ø—Ä–æ—Ü–µ—Å—Å –∑–∞—Ç—É—Ö–∞–Ω–∏—è —Ç–µ–æ—Ä–µ—Ç–∏—á–µ—Å–∫–∏ –±—É–¥–µ—Ç –¥–ª–∏—Ç—å—Å—è –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –¥–æ–ª–≥–æ. –ù–æ —Ç–∞–∫ –∂–µ —Ç–µ–æ—Ä–µ—Ç–∏—á–µ—Å–∫–∏ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –¥–æ–ª–≥–æ –±—É–¥–µ—Ç –ø—Ä–æ–∏—Å—Ö–æ–¥–∏—Ç—å –ø—Ä–æ—Ü–µ—Å—Å –∏ –ø—Ä–∏ —Å–æ–µ–¥–∏–Ω–µ–Ω–∏–∏ —á–µ—Ä–µ–∑ —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏–µ. –ü–æ—ç—Ç–æ–º—É —è –∏ –≤–∏–¥–µ–ª, —á—Ç–æ —Å–º—ã—Å–ª —É –∑–∞–¥–∞—á–∏ –ø–æ—è–≤–∏—Ç—Å—è —Ç–æ–ª—å–∫–æ, –µ—Å–ª–∏ –Ω–∞—Ä—è–¥—É —Å –∫–æ–ª–µ–±–∞—Ç–µ–ª—å–Ω—ã–º –ø—Ä–æ—Ü–µ—Å—Å–æ–º –±—É–¥–µ—Ç –∏–¥—Ç–∏ –ø—Ä–æ—Ü–µ—Å—Å –∏–∑–ª—É—á–µ–Ω–∏—è. –¢–æ–≥–¥–∞ –º—ã –∏ –ø—Ä–∏—Ö–æ–¥–∏–º –∫ —Ä–µ–∑—É–ª—å—Ç–∞—Ç—É –¢–°. –í–æ—Ç —Ç–∞–∫–∞—è "—Å–æ–æ–±—Ä–∞–∑–∏—Ç–µ–ª—å–Ω–æ—Å—Ç—å" –±—ã–ª–∞ —É –º–µ–Ω—è. –ò —è –Ω–µ —Å—á–∏—Ç–∞—é, —á—Ç–æ –º–æ–π –≤–∞—Ä–∏–∞–Ω—Ç —Ç–∞–∫–æ–π —É–∂ –Ω–µ–∫–æ—Ä—Ä–µ–∫—Ç–Ω—ã–π. –Ø –æ–ø–∏—Ä–∞–ª—Å—è –Ω–∞ —Ç–æ, —á—Ç–æ –∏–¥–µ–∞–ª—å–Ω—ã–π –ø—Ä–æ–≤–æ–¥–Ω–∏–∫ –∏–º–µ–µ—Ç –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å. –ò —ç—Ç–æ –Ω–∏–∫—Ç–æ –Ω–µ –æ—Ç—Ä–∏—Ü–∞–ª. –ü–æ–ø—É—Ç–Ω–æ, –∏–º–µ–Ω–Ω–æ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å —Ä–µ–∞–ª—å–Ω–æ –∏ –æ–≥—Ä–∞–Ω–∏—á–∏–≤–∞–µ—Ç —Ç–æ—Ç –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –±–æ–ª—å—à–æ–π —Ç–æ–∫, –Ω–∞ –∫–æ—Ç–æ—Ä—ã–π —É–∫–∞–∑—ã–≤–∞–ª Gudd-Head. –î–∞ –∏, –≤–æ–æ–±—â–µ, –ª—é–±–æ–π –ø—Ä–æ–≤–æ–¥–Ω–∏–∫ –æ–±–ª–∞–¥–∞–µ—Ç —Å–≤–æ–π—Å—Ç–≤–æ–º –∏–∑–ª—É—á–∞—Ç—å —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω—ã–µ –≤–æ–ª–Ω—ã –ø—Ä–∏ –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω—ã—Ö —É—Å–ª–æ–≤–∏—è—Ö (–ø—Ä–∞–≤–¥–∞, Slabovik —É—Ç–≤–µ—Ä–∂–¥–∞–ª, —á—Ç–æ –º–∞–ª–∞—è —Ä–∞–º–∫–∞ –≤ –∏–¥–µ–∞–ª—å–Ω–æ–º –≤–∏–¥–µ –∏–∑–ª—É—á–∞—Ç—å –Ω–µ –º–æ–∂–µ—Ç, –ø—Ä–∞–≤–¥–∞ –ø–æ—Å–ª–µ –ø—Ä–æ–≤–µ–¥–µ–Ω–∏—è –Ω–µ–±–æ–ª—å—à–æ–≥–æ –ª–∏–∫–±–µ–∑–∞ –∏–∑–º–µ–Ω–∏–ª —Å–≤–æ—é —Ç–æ—á–∫—É –∑—Ä–µ–Ω–∏—è) viewtopic.php?p=1819440#p1819440–ê –¥–ª—è —ç—Ç–æ–≥–æ, –≤—ã—Ä–∞–∂–µ–Ω–∏–µ –≤ —É—Å–ª–æ–≤–∏–∏ "–ü–æ—Ç–µ—Ä—è–º–∏ –≤ –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–∞—Ö –ø—Ä–µ–Ω–µ–±—Ä–µ–≥–∞–µ–º" —Å–ª–µ–¥—É–µ—Ç —Ç–æ–≥–¥–∞ –ø–æ–Ω–∏–º–∞—Ç—å, –∫–∞–∫ –æ—Ç—Å—É—Ç—Å—Ç–≤–∏–µ –æ–º–∏—á–µ—Å–∫–∏—Ö –ø–æ—Ç–µ—Ä—å (—è, –∫—Å—Ç–∞—Ç–∏, —Ç–æ–ª—å–∫–æ —Ç–∞–∫ –∏ –ø–æ–Ω—è–ª —Å —Å–∞–º–æ–≥–æ –Ω–∞—á–∞–ª–∞ –∏ –¥—É–º–∞—é, —á—Ç–æ —ç—Ç–æ –≤–ø–æ–ª–Ω–µ –ª–æ–≥–∏—á–Ω–æ). –ê –ø–æ—á–µ–º—É –±—ã –∏ –Ω–µ—Ç, –µ—Å–ª–∏ "–∑–∞–¥–∞—á–∞ –Ω–∞ —Å–æ–æ–±—Ä–∞–∑–∏—Ç–µ–ª—å–Ω–æ—Å—Ç—å" –∏ —ç—Ç–æ –ø—Ä–∏–≤–æ–¥–∏—Ç –∫ –æ–±—ä—è—Å–Ω–µ–Ω–∏—é –≤—ã—á–∏—Å–ª–µ–Ω–Ω–æ–≥–æ —Ä–µ–∑—É–ª—å—Ç–∞—Ç–∞. –¢.–µ., —è –ø–æ–∫–∞–∑–∞–ª, –∫–æ–≥–¥–∞ —Ç–∞–∫–æ–π —Ä–µ–∑—É–ª—å—Ç–∞—Ç –≤–æ–∑–º–æ–∂–µ–Ω. –ü—Ä–∏–Ω—è—Ç—å, —á—Ç–æ –∏–∑–ª—É—á–µ–Ω–∏—è –Ω–µ—Ç, —è –¥—É–º–∞—é, –º–æ–∂–Ω–æ —Ç–æ–ª—å–∫–æ —Ñ–æ—Ä–º–∞–ª—å–Ω–æ. –ò Slabovik –¥–ª—è —ç—Ç–æ–≥–æ —Å–ª—É—á–∞—è –ø–µ—Ä–≤—ã–º –¥–∞–ª –ø—Ä–∞–≤–∏–ª—å–Ω—ã–π –æ—Ç–≤–µ—Ç, –æ–¥–Ω–∞–∫–æ –æ–Ω –Ω–µ –ø—Ä–∏–≤–æ–¥–∏—Ç –∫ –Ω—É–∂–Ω–æ–º—É —Å–º—ã—Å–ª—É —Ä–µ—à–µ–Ω–∏—è –∑–∞–¥–∞—á–∏ –≤ –ø–æ–Ω–∏–º–∞–Ω–∏–∏ –¢–°. –¢–µ–ø–µ—Ä—å –ø–æ –ø–æ–≤–æ–¥—É –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞—Ç–µ–ª—è (—Ç.–µ. 0,707 U). –í–æ—Ç —Å—Ö–µ–º–∞:  –í—Å–µ –¥–µ—Ç–∞–ª–∏ –∏–¥–µ–∞–ª—å–Ω—ã–µ. –û–ø—è—Ç—å –∂–µ, —É—Å–ª–æ–≤–Ω–æ –ø—Ä–∏–Ω–∏–º–∞–µ–º, —á—Ç–æ –∏–∑–ª—É—á–µ–Ω–∏—è –∏ –¥—Ä—É–≥–∏—Ö –ø–æ—Ç–µ—Ä—å —ç–Ω–µ—Ä–≥–∏–∏ –Ω–µ—Ç. –¢–∞–∫ –≤–æ—Ç, –∑–∞–º—ã–∫–∞—è –Ω–∞ –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω–æ–µ –≤—Ä–µ–º—è –∫–ª—é—á –∏ —Ä–∞–∑–º—ã–∫–∞—è –µ–≥–æ, –º—ã –º–æ–∂–µ–º –ø–æ–ª—É—á–∏—Ç—å –Ω–µ —Ç–æ–ª—å–∫–æ —Ä–∞–≤–Ω—ã–µ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏—è –ø–æ 0,707 U, –Ω–æ –∏ –ø–æ–ª–Ω–æ—Å—Ç—å—é –ø–µ—Ä–µ–∫–∞—á–∞—Ç—å —ç–Ω–µ—Ä–≥–∏—é –∏–∑ –ø–µ—Ä–≤–æ–≥–æ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ –≤–æ –≤—Ç–æ—Ä–æ–π. –ò–º–µ–µ—Ç—Å—è –≤–≤–∏–¥—É –æ–¥–∏–Ω —Ç–∞–∫—Ç —Ä–∞–±–æ—Ç—ã —É—Å—Ç—Ä–æ–π—Å—Ç–≤–∞ - –≤–∫–ª—é—á–µ–Ω–∏–µ –∫–ª—é—á–∞ –Ω–∞ –Ω—É–∂–Ω–æ–µ –≤—Ä–µ–º—è –∏ –≤—ã–∫–ª—é—á–µ–Ω–∏–µ. –ù–æ —ç—Ç–æ –ø—Ä–æ—Å—Ç–æ –∏–ª–ª—é—Å—Ç—Ä–∞—Ü–∏—è, –∫–∞–∫ —ç—Ç–æ–≥–æ –¥–æ—Å—Ç–∏—á—å –∏ –∫ –Ω–∞—à–µ–π –∑–∞–¥–∞—á–µ –æ—Ç–Ω–æ—à–µ–Ω–∏—è –Ω–µ –∏–º–µ–µ—Ç.
| –í–ª–æ–∂–µ–Ω–∏—è: |
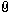 15.GIF [1.13 KiB]
15.GIF [1.13 KiB]
–°–∫–∞—á–∏–≤–∞–Ω–∏–π: 2341
|
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
Gudd-Head

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 10:43:50 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 67
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1065
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —Å–µ–Ω 18, 2008 12:27:21
–°–æ–æ–±—â–µ–Ω–∏–π: 19930
–û—Ç–∫—É–¥–∞: –°—Ç–æ–ª–∏—Ü–∞ –ú–∏—Ä–∞ –°–∞–Ω–∫—Ç-–ü–µ—Ç–µ—Ä–±—É—Ä–≥
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ú–µ–¥–∞–ª–∏: 1

|
Slabovik –ø–∏—Å–∞–ª(–∞): –ë—Ä–∞–≤–æ! –ü–æ–¥—É–º–∞–ª, —á—Ç–æ-—Ç–æ –¥–∞–≤–Ω–æ —è —Å –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞–º–∏ –Ω–µ –∏–≥—Ä–∞–ª—Å—è  –ò –¥–∞–∂–µ –Ω–µ –ø–æ–ª–µ–Ω–∏–ª—Å—è –Ω–∞–±–∏—Ç—å —Å–æ–æ—Ç–≤. —Ñ–æ—Ä–º—É–ª—ã –≤ –í–æ—Ä–¥–µ (—à—Ç–∞—Ç–Ω–∞—è –≤–æ—Ä–¥–æ–≤—Å–∫–∞—è —à—Ç—É–∫–∞ –¥–ª—è —ç—Ç–æ–≥–æ ‚Äî –∫–∞–∫–∞. –Ý–µ–∫–æ–º–µ–Ω–¥—É—é –ø–æ—Å—Ç–∞–≤–∏—Ç—å –ø–ª–∞–≥–∏–Ω? Math Type). rl55 –ø–∏—Å–∞–ª(–∞): –ø–æ–ª–Ω–æ—Å—Ç—å—é –ø–µ—Ä–µ–∫–∞—á–∞—Ç—å —ç–Ω–µ—Ä–≥–∏—é –∏–∑ –ø–µ—Ä–≤–æ–≥–æ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ –≤–æ –≤—Ç–æ—Ä–æ–π. –ü–æ–ª–Ω–æ—Å—Ç—å—é –Ω–µ –ø–æ–ª—É—á–∏—Ç—Å—è, —ç—Ç–æ –≤—Å—ë-—Ç–∞–∫–∏ –ø–æ–Ω–∏–∂–∞—é—â–∏–π –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞—Ç–µ–ª—å ‚Äî –ø—Ä–∏ —Ä–∞–≤–µ–Ω—Å—Ç–≤–µ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–π –Ω–∞ –∫–æ–Ω–¥—ë—Ä–∞—Ö —Ç–æ–∫ —á–µ—Ä–µ–∑ –¥—Ä–æ—Å—Å–µ–ª—å –Ω–µ –ø–æ—Ç–µ—á—ë—Ç 
_________________
[ –í—Å—ë –¥–µ–ª–æ –Ω–µ —Å—Ç–æ–ª—å–∫–æ –≤ –≤–∞—à–µ–π –≥–ª—É–ø–æ—Å—Ç–∏, —Å–∫–æ–ª—å–∫–æ –≤ –º–æ–µ–π –≥–µ–Ω–∏–∞–ª—å–Ω–æ—Å—Ç–∏ ] [ –ü—Ä–∞–≤–∏–ª—å–Ω–æ –∑–∞–¥–∞–Ω–Ω—ã–π –≤–æ–ø—Ä–æ—Å —Å–æ–¥–µ—Ä–∂–∏—Ç –≤ —Å–µ–±–µ –ø–æ–ª–æ–≤–∏–Ω—É –æ—Ç–≤–µ—Ç–∞ ]
–ò–∑–º–µ—Ä–∏—Ç—å –Ω–Ω–Ω–∞–¥–∞?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
rl55

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 11:15:11 |
|
–ö–∞—Ä–º–∞: 79
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1412
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä —Ñ–µ–≤ 13, 2013 21:59:40
–°–æ–æ–±—â–µ–Ω–∏–π: 16166
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
Gudd-Head писал(а): Полностью не получится, это всё-таки понижающий преобразователь — при равенстве напряжений на кондёрах ток через дроссель не потечёт У меня преобразователь не в классическом смысле: rl55 писал(а): Имеется ввиду один такт работы устройства - включение ключа на нужное время и выключение. Замыкаем ключ, начинается перезарядка конденсаторов. При равенстве напряжений на конденсаторах (0,5 U) ток в индуктивности максимальный, максимальна запасенная энергия. Ток не прекращается, продолжается разрядка первого конденсатора и зарядка второго. В момент, когда первый разрядится полностью, а второй зарядится до +U, отключаем ключ. Вот и все. Могу попутно объяснить, как получается 0,707 U. В момент, когда первый конденсатор разрядился до 0,707 U, выключаем ключ. Второй конденсатор дозарядится до 0,707 U за счет накопленной энергии магнитного поля в индуктивности (через диод). Энергия распределится поровну (именно по 0,707 U по напряжению на каждом конденсаторе), чего так усиленно хотел vem566, только не знал, как это сделать, кроме как математически. И я уже писал, что в предлагаемой задаче это сделать невозможно.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
–ó–≤–µ–∑–¥–æ—á—ë—Ç

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 13:12:10 |
|
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü—Ç –∞–≤–≥ 16, 2013 14:44:30
–°–æ–æ–±—â–µ–Ω–∏–π: 7
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–ø–æ–¥–µ–ª–∏—Ç—å —ç–Ω–µ—Ä–≥–∏—é –ø–æ—Ä–æ–≤–Ω—É –Ω–µ –æ–±–µ—â–∞—é, –∞ –≤–æ—Ç —Å–æ—Ö—Ä–∞–Ω–∏—Ç—å –º–æ–∂–Ω–æ —Ç–∞–∫  –ò –Ω–µ –Ω–∞–¥–æ –ª–æ–≤–∏—Ç—å –º–æ–º–µ–Ω—Ç –æ—Ç–∫–ª—é—á–µ–Ω–∏—è —Ä—É–±–∏–ª—å–Ω–∏–∫–∞. 
| –í–ª–æ–∂–µ–Ω–∏—è: |
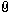 cap.GIF [1.21 KiB]
cap.GIF [1.21 KiB]
–°–∫–∞—á–∏–≤–∞–Ω–∏–π: 2119
|
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
rl55

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 13:29:52 |
|
–ö–∞—Ä–º–∞: 79
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1412
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä —Ñ–µ–≤ 13, 2013 21:59:40
–°–æ–æ–±—â–µ–Ω–∏–π: 16166
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–î–∞, —ç–Ω–µ—Ä–≥–∏—è —Å–æ—Ö—Ä–∞–Ω–∏—Ç—Å—è –∏ –ø–æ–ª–Ω–æ—Å—Ç—å—é –ø–µ—Ä–µ–π–¥–µ—Ç –≤–æ –≤—Ç–æ—Ä–æ–π –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä. –ù–æ –Ω–µ –ø–æ–¥–µ–ª–∏—Ç—Å—è. –í–∏–¥–∏—Ç–µ, –∫–∞–∫–æ–π —É –Ω–∞—Å —Ñ–æ—Ä—É–º —É–º–Ω—ã–π...  –ê –ø–æ –ø–æ–≤–æ–¥—É "–ª–æ–≤–∏—Ç—å –º–æ–º–µ–Ω—Ç –æ—Ç–∫–ª—é—á–µ–Ω–∏—è —Ä—É–±–∏–ª—å–Ω–∏–∫–∞" - —Ç–∞–∫ —ç—Ç–æ –∂–µ –∞–±—Å—Ç—Ä–∞–∫—Ç–Ω–∞—è –º–æ–¥–µ–ª—å, –∫—Ç–æ –µ–≥–æ —Ä–µ–∞–ª—å–Ω–æ –ª–æ–≤–∏—Ç—å –±—É–¥–µ—Ç...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
O_l_e_g

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 17:45:35 |
|
| –ù–∞—à–µ–ª —Ç—Ä–∞–Ω–∑–∏—Å—Ç–æ—Ä. –ü–æ–Ω—é—Ö–∞–ª. |
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –í—Ç –¥–µ–∫ 27, 2011 01:13:21
–°–æ–æ–±—â–µ–Ω–∏–π: 191
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
Slabovik
–û—à–∏–±–∫–∞ –ø—Ä–∏ –≤—ã—á–∏—Å–ª–µ–Ω–∏–∏ –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞. –ü–æ—Å–º–æ—Ç—Ä–∏—Ç–µ –ø–æ–¥ –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–º —Ç–æ–∫ –≤ –∫–≤–∞–¥—Ä–∞—Ç–µ –∏ –∫–æ–≥–¥–∞ –≤—ã–Ω–æ—Å–∏–º –∑–∞ –∏–Ω—Ç–µ–≥—Ä–∞–ª —Ç–æ –Ω–µ —Ç–æ–ª—å–∫–æ U –≤ –∫–≤–∞–¥—Ä–∞—Ç–µ –Ω–æ –∏ —Ä–∞–∑–¥–µ–ª–∏—Ç—å –Ω–∞–¥–æ –Ω–∞ R –≤ –∫–≤–∞–¥—Ä–∞—Ç–µ. –¢–∞–∫ —á—Ç–æ —ç–Ω–µ—Ä–≥–∏—è –Ω–∞ —Ç–µ–ø–ª–æ –±—É–¥–µ—Ç –∑–∞–≤–∏—Å–µ—Ç—å –æ—Ç —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏—è –ø–æ—Ç–µ—Ä—å. –ë–æ–ª–µ–µ —Ç–æ–≥–æ –æ–±—ä—è—Å–Ω—è—Ç—å –¥–∞–Ω–Ω—ã–π —ç—Ñ—Ñ–µ–∫—Ç –ø–æ—Ç–µ—Ä—è–º–∏ –ø—Ä–æ—Å—Ç–æ —Å–º–µ—à–Ω–æ. –í–æ–∑—å–º–∏—Ç–µ —Ç–µ–ø–µ—Ä—å —ç—Ç–∏ 2 –∑–∞—Ä—è–∂–µ–Ω–Ω—ã—Ö –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ –∏ —Å–æ–µ–¥–∏–Ω–∏—Ç–µ –ø–æ—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª—å–Ω–æ –∏ –ø–æ—Å—á–∏—Ç–∞–π—Ç–µ –ø–æ —Ñ–æ—Ä–º—É–ª–µ {q=CU –∏ E=(C*U^2)/2} –≤—ã –µ—â–µ –±–æ–ª—å—à–µ —É–¥–∏–≤–∏—Ç–µ—Å—å. –ê –≤–æ–æ–±—â–µ —à–∫–æ–ª—å–Ω—ã–π –∫—É—Ä—Å —Ñ–∏–∑–∏–∫–∏ –Ω–µ–ø—Ä–æ—Ç–∏–≤–æ—Ä–µ—á–∏–≤. –ê —ç—Ç–æ –∑–Ω–∞—á–∏—Ç –≤—Å–µ —è–≤–ª–µ–Ω–∏—è –º–æ–∂–Ω–æ –æ–±—ä—è—Å–Ω–∏—Ç—å –±–µ–∑ —É—á–µ—Ç–∞ –ø–æ—Ç–µ—Ä—å. –ú—ã –∂–µ –∏–∑—É—á–∞–µ–º —Ä–∞–±–æ—Ç—É –º–∞—è—Ç–Ω–∏–∫–∞, –Ω–æ —Ä–∞–∑–≤–µ –∫—Ç–æ –Ω–∏–±—É–¥—å —É—á–∏—Ç—ã–≤–∞–µ—Ç —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏–µ –≤–æ–∑–¥—É—Ö–∞. –ü–æ—Ç–µ—Ä–∏ –Ω–∞—á–∏–Ω–∞—é—Ç –∏—Å–ø–æ–ª—å–∑–æ–≤–∞—Ç—å –≤ —à–∫–æ–ª—å–Ω–æ–π —Ñ–∏–∑–∏–∫–µ –∫–æ–≥–¥–∞ –Ω–∞–¥–æ –æ–±—ä—è—Å–Ω–∏—Ç—å –ø—Ä–∏—á–∏–Ω—É –∑–∞—Ç—É—Ö–∞–Ω–∏—è –∫–æ–ª–µ–±–∞–Ω–∏–π –∏–ª–∏ –∫–æ–≥–¥–∞ –ø—Ä–∏—Ö–æ–¥–∏—Ç—å—Å—è –¥–µ–ª–∏—Ç—å –Ω–∞ –Ω–æ–ª—å. –ù–∞ –Ω–æ–ª—å –¥–µ–ª–∏—Ç—å –Ω–µ–ª—å–∑—è -- –∑–Ω–∞—á–∏—Ç —á–µ–≥–æ —Ç–æ –Ω–µ —É—á–ª–∏ ... –µ—â–µ –≤ –∑–∞–¥–∞—á–∞—Ö –Ω–∞ —Ç–µ–ø–ª–æ –ë–æ–ª–µ–µ —Ç–æ–≥–æ –≤—ã–¥–µ–ª—è—é—â–µ–µ—Å—è —Ç–µ–ø–ª–æ –Ω–µ –º–æ–∂–µ—Ç –Ω–µ –∑–∞–≤–∏—Å–µ—Ç—å –æ—Ç —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏—è –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–∞. –ê –ø–æ—Å–∫–æ–ª—å–∫—É –∑–¥–µ—Å—å –∏–¥–µ—Ç "—Å—Ç—Ä–æ–≥–∞—è –ø–æ–ª–æ–≤–∏–Ω–∞ –ø–æ—Ç–µ—Ä–∏ —ç–Ω–µ—Ä–≥–∏–∏" —Ç–æ –æ–Ω–∞ –Ω–∏–∫–∞–∫ –Ω–µ –º–æ–∂–µ—Ç –±—ã—Ç—å —Å–≤—è–∑–∞–Ω–∞ —Å —Ç–µ–ø–ª–æ–≤—ã–º–∏ –ø–æ—Ç–µ—Ä—è–º–∏, –≤ —Ç–æ–º —á–∏—Å–ª–µ –∏ —Å –¥—Ä—É–≥–∏–º–∏ –ø–æ—Ç–µ—Ä—è–º–∏. –í —Å–∞–º–æ–º –¥–µ–ª–µ –µ—Å–ª–∏ –º—ã —Å–æ–µ–¥–∏–Ω–∏–º —Ç–µ –∂–µ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä—ã –Ω–∏—Ö—Ä–æ–º–æ–≤–æ–π –ø—Ä–æ–≤–ª–∫–æ–π –æ—Ç —É—Ç—é–≥–∞ –∏–ª–∏ –ø—Ä–æ–≤–æ–¥ –±—É–¥–µ—Ç –Ω–µ—Å–∫–æ–ª—å–∫–æ –∫–∏–ª–æ–º–µ—Ç—Ä–æ–≤, –Ω–µ—É–∂–µ–ª–∏ –∏ –≤ —ç—Ç–æ–º —Å–ª—É—á–∞–µ –ø–æ—Ç–µ—Ä–∏ —Å–æ—Å—Ç–∞–≤—è—Ç –ø–æ–ª–æ–≤–∏–Ω—É. –ò–ª–∏ –ø–æ–ª–æ–≤–∏–Ω—É -- —ç—Ç–æ —Ç–æ–ª—å–∫–æ –¥–ª—è –∏–¥–µ–∞–ª—å–Ω–æ–≥–æ —Å–ª—É—á–∞—è –∫–æ–≥–¥–∞ –≤ –∑–∞–¥–∞—á–µ –≥–æ–≤–æ—Ä–∏—Ç—å—Å—è —á—Ç–æ –ø–æ—Ç–µ—Ä—å –Ω–µ—Ç –Ω—É –∏ –ø–ª—é—Å –µ—â–µ —Ç–∞–º –Ω–∞ –Ω–∏—Ö—Ä–æ–º –Ω–∞ 5 –∫–º –ø—Ä–æ–≤–æ–¥–∞ —ç—Ç–æ –µ—â–µ –ø–æ—Ç–µ—Ä–∏. –Ø—Å–Ω–æ —á—Ç–æ —ç–Ω–µ—Ä–≥–∏—è –∑–∞—Ä—è–∂–µ–Ω–Ω–æ–≥–æ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ —É–º–µ–Ω—å—à–∏–ª–∞—Å—å. –í–æ—Ç —Ç–æ–ª—å–∫–æ –∫—É–¥–∞ –æ–Ω–∞ –¥–µ–ª–∞—Å—å –Ω–µ –Ω–∞–¥–æ –æ–±—ä—è—Å–Ω—è—Ç—å –ø–æ—Ç–µ—Ä—è–º–∏ –Ω–∞ —Ç–µ–ø–ª–æ –ø–æ–ª—É—á–∏—Ç–µ –ø—Ä–æ—Ç–∏–≤–æ—Ä–µ—á–∏–µ —á—Ç–æ –ø–æ—Ç–µ—Ä–∏ –Ω–µ –∑–∞–≤–∏—Å—è—Ç –æ—Ç —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏—è –∏ –¥–ª–∏–Ω–Ω—ã —Å–æ–µ–¥–∏–Ω–∏—Ç–µ–ª—å–Ω—ã—Ö –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–æ–≤.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
–ö–Ý–ê–ú

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 18:29:12 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 139
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 2918
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 10, 2008 22:01:02
–°–æ–æ–±—â–µ–Ω–∏–π: 24586
–û—Ç–∫—É–¥–∞: –ú–æ—Å–∫–æ–≤—Å–∫–∞—è –æ–±–ª–∞—Å—Ç—å, –§—Ä—è–∑–∏–Ω–æ
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
O_l_e_g –ø–∏—Å–∞–ª(–∞): –¢–∞–∫ —á—Ç–æ —ç–Ω–µ—Ä–≥–∏—è –Ω–∞ —Ç–µ–ø–ª–æ –±—É–¥–µ—Ç –∑–∞–≤–∏—Å–µ—Ç—å –æ—Ç —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏—è –ø–æ—Ç–µ—Ä—å. –ë–æ–ª–µ–µ —Ç–æ–≥–æ –æ–±—ä—è—Å–Ω—è—Ç—å –¥–∞–Ω–Ω—ã–π —ç—Ñ—Ñ–µ–∫—Ç –ø–æ—Ç–µ—Ä—è–º–∏ –ø—Ä–æ—Å—Ç–æ —Å–º–µ—à–Ω–æ.....
....–ø–æ—Å–∫–æ–ª—å–∫—É –∑–¥–µ—Å—å –∏–¥–µ—Ç "—Å—Ç—Ä–æ–≥–∞—è –ø–æ–ª–æ–≤–∏–Ω–∞ –ø–æ—Ç–µ—Ä–∏ —ç–Ω–µ—Ä–≥–∏–∏" —Ç–æ –æ–Ω–∞ –Ω–∏–∫–∞–∫ –Ω–µ –º–æ–∂–µ—Ç –±—ã—Ç—å —Å–≤—è–∑–∞–Ω–∞ —Å —Ç–µ–ø–ª–æ–≤—ã–º–∏ –ø–æ—Ç–µ—Ä—è–º–∏, –≤ —Ç–æ–º —á–∏—Å–ª–µ –∏ —Å –¥—Ä—É–≥–∏–º–∏ –ø–æ—Ç–µ—Ä—è–º–∏. –∞)–ë–µ—Ä–µ–º –∏–¥–µ–∞–ª—å–Ω—ã–π –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä –∑–∞—Ä—è–∂–µ–Ω–Ω—ã–π –¥–æ U –∏ –∑–∞–∫–æ—Ä–∞—á–∏–≤–∞–µ–º –µ–≥–æ –∏–¥–µ–∞–ª—å–Ω—ã–º –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–æ–º. –±)–ë–µ—Ä–µ–º –¥—Ä—É–≥–æ–π –∏–¥–µ–∞–ª—å–Ω—ã–π –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä –∑–∞—Ä—è–∂–µ–Ω–Ω—ã–π –¥–æ U –∏ –∑–∞–∫–æ—Ä–∞—á–∏–≤–∞–µ–º –µ–≥–æ –∏–¥–µ–∞–ª—å–Ω—ã–º –∏—Å—Ç–æ—á–Ω–∏–∫–æ–º –≠–î–° —Å –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ–º U/2, —Å–æ–±–ª—é–¥–∞—è –ø–æ–ª—è—Ä–Ω–æ—Å—Ç—å –∏—Å—Ç–æ—á–Ω–∏–∫–∞ –∏ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ –∏–¥–µ–Ω—Ç–∏—á–Ω–æ–π. –≠–Ω–µ—Ä–≥–∏—è –≤ –æ–±–æ–∏—Ö —Å–ª—É—á–∞—è—Ö –±—É–¥–µ—Ç –∫–æ–Ω–µ—á–Ω–æ–π –∏ –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω–æ–π.–ù–µ–∑–∞–≤–∏—Å–∏–º–æ–π –æ—Ç —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏—è, –∫–æ—Ç–æ—Ä–æ–µ —Ä–∞–≤–Ω–æ –Ω—É–ª—é. –ú–æ—â–Ω–æ—Å—Ç—å, –ø—Ä–∞–≤–¥–∞, –±—É–¥–µ—Ç –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ–π.... –í–µ–¥—å –ø–æ—Å—Ç–æ—è–Ω–Ω–∞—è –≤—Ä–µ–º–µ–Ω–∏ —Ç–∞–∫–æ–π —Ü–µ–ø–∏ –±—É–¥–µ—Ç —Ä–∞–≤–Ω–∞ –Ω—É–ª—é... –ö–∞–∫ —É –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏. –ü–ª–æ—â–∞–¥—å –µ–¥–∏–Ω–∏—á–Ω–∞—è, –∞ –º–æ—â–Ω–æ—Å—Ç—å –±–µ—Å–∫–æ–Ω–µ—á–Ω–∞—è... –ú–æ–∂–µ—Ç —ç—Ç–æ –æ–Ω–∞?  –ó–´. –ü–æ–∑–æ—Ä. –ú–Ω–µ, –¥–≤–æ–µ—á–Ω–∏–∫—É –ü–µ—Ä–µ—Å—Ç—É–∫–∏–Ω—É... –¢–∞–∫ –æ–±–ª–∞–∂–∞—Ç—å—Å—è –≤ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω–æ–π –∑–∞–¥–∞—á–µ...  –ì–ª–∞–≤–Ω–æ–µ —Å—Ä–∞–∑—É –ø–æ—Å—Ç—Ä–æ–∏—Ç—å –º–æ–¥–µ–ª—å... 
–ü–æ—Å–ª–µ–¥–Ω–∏–π —Ä–∞–∑ —Ä–µ–¥–∞–∫—Ç–∏—Ä–æ–≤–∞–ª–æ—Å—å –ö–Ý–ê–ú –°–± –æ–∫—Ç 26, 2013 18:46:22, –≤—Å–µ–≥–æ —Ä–µ–¥–∞–∫—Ç–∏—Ä–æ–≤–∞–ª–æ—Å—å 1 —Ä–∞–∑.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
rl55

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 18:46:19 |
|
–ö–∞—Ä–º–∞: 79
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1412
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä —Ñ–µ–≤ 13, 2013 21:59:40
–°–æ–æ–±—â–µ–Ω–∏–π: 16166
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
O_l_e_g, –≤—ã—á–∏—Å–ª—è–ª –Ω–µ Slabovik, –∞ Gudd-Head.
–Ø, —Ö–æ—Ç—è –∏ –ª–µ—Ç 40 —É–∂–µ –Ω–µ –≤–∏–¥–µ–ª –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤, –≤—Ä–æ–¥–µ –±—ã –Ω–µ –≤–∏–∂—É –æ—à–∏–±–∫–∏.
–ï—Å–ª–∏ —É—á–µ—Å—Ç—å –≤—Å–µ R - –ø–µ—Ä–µ–¥ –∑–Ω–∞–∫–æ–º –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞, R^2, –∫–∞–∫ –≤—ã —É–∂–µ —Å–∫–∞–∑–∞–ª–∏ –∏ R –≤ –ø–æ–∫–∞–∑–∞—Ç–µ–ª–µ —Å—Ç–µ–ø–µ–Ω–∏ e, —Ç–æ –≤—Å–µ R —Å–æ–∫—Ä–∞—Ç—è—Ç—Å—è.
–ü—Ä–æ–≤–µ—Ä—å—Ç–µ, –º–æ–∂–µ—Ç —è –æ—à–∏–±–∞—é—Å—å. –ö–æ–≥–¥–∞-—Ç–æ –ª–µ–≥–∫–æ —Å–ø—Ä–∞–≤–ª—è–ª—Å—è —Å –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞–º–∏, –Ω–æ –±–µ–∑ –ø—Ä–∞–∫—Ç–∏–∫–∏ –º–Ω–æ–≥–æ–µ –∑–∞–±—ã–ª.
–ü—Ä–∏ —Å–æ–µ–¥–∏–Ω–µ–Ω–∏–∏ —á–µ—Ä–µ–∑ —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏–µ –ø–æ –∑–∞–∫–æ–Ω—É —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è –∑–∞—Ä—è–¥–∞ –∑–∞—Ä—è–¥ —Ä–∞–∑–¥–µ–ª–∏—Ç—Å—è –ø–æ–ø–æ–ª–∞–º, –Ω–∞–ø—Ä—è–∂–µ–Ω–∏—è –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞—Ö —É–º–µ–Ω—å—à–∞—Ç—Å—è –≤ 2 —Ä–∞–∑–∞, —ç–Ω–µ—Ä–≥–∏—è –Ω–∞ –∫–∞–∂–¥–æ–º - –≤ —á–µ—Ç—ã—Ä–µ —Ä–∞–∑–∞, –æ–±—â–∞—è —ç–Ω–µ—Ä–≥–∏—è –≤ 2 —Ä–∞–∑–∞.
–ü–æ –∑–∞–∫–æ–Ω—É —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è —ç–Ω–µ—Ä–≥–∏–∏ –ø–æ–ª–æ–≤–∏–Ω–∞ –Ω–µ–¥–æ—Å—Ç–∞—é—â–µ–π —ç–Ω–µ—Ä–≥–∏–∏ —É–π–¥–µ—Ç –≤ —Ç–µ–ø–ª–æ.
–í—Ä–æ–¥–µ –±—ã, —Ç–æ–∂–µ –Ω–µ–ø—Ä–æ—Ç–∏–≤–æ—Ä–µ—á–∏–≤–æ.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
El-Eng

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 19:33:58 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 97
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1584
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 26, 2012 14:44:34
–°–æ–æ–±—â–µ–Ω–∏–π: 3736
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ú–µ–¥–∞–ª–∏: 1

|
rl55 –ø–∏—Å–∞–ª(–∞): –ü—Ä–∏ —Å–æ–µ–¥–∏–Ω–µ–Ω–∏–∏ —á–µ—Ä–µ–∑ —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏–µ –ø–æ –∑–∞–∫–æ–Ω—É —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è –∑–∞—Ä—è–¥–∞ –∑–∞—Ä—è–¥ —Ä–∞–∑–¥–µ–ª–∏—Ç—Å—è –ø–æ–ø–æ–ª–∞–º, –Ω–∞–ø—Ä—è–∂–µ–Ω–∏—è –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞—Ö —É–º–µ–Ω—å—à–∞—Ç—Å—è –≤ 2 —Ä–∞–∑–∞, —ç–Ω–µ—Ä–≥–∏—è –Ω–∞ –∫–∞–∂–¥–æ–º - –≤ —á–µ—Ç—ã—Ä–µ —Ä–∞–∑–∞, –æ–±—â–∞—è —ç–Ω–µ—Ä–≥–∏—è –≤ 2 —Ä–∞–∑–∞. –ü–æ –∑–∞–∫–æ–Ω—É —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è —ç–Ω–µ—Ä–≥–∏–∏ –ø–æ–ª–æ–≤–∏–Ω–∞ –Ω–µ–¥–æ—Å—Ç–∞—é—â–µ–π —ç–Ω–µ—Ä–≥–∏–∏ —É–π–¥–µ—Ç –≤ —Ç–µ–ø–ª–æ. –ö–æ–º—É –∏–Ω—Ç–µ—Ä–µ—Å–Ω–æ: –ø—Ä–æ–º–æ–¥–µ–ª–∏—Ä–æ–≤–∞–ª –∑–∞–¥–∞—á–∫—É –Ω–∞ PSPICE. –ï–º–∫–æ—Å—Ç–∏ –±—ã–ª–∞ –ø–æ —Ñ–∞—Ä–∞–¥–µ. –ù–∞–ø—Ä—è–∂–µ–Ω–∏–µ - 1 –∫–∏–ª–æ–≤–æ–ª—å—Ç. –Ý–µ–∑—É–ª—å—Ç–∞—Ç: –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ —É–º–µ–Ω—å—à–∞–µ—Ç—Å—è –≤ –¥–≤–∞ —Ä–∞–∑–∞ –¥–ª—è —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏—è –∑–∞–º—ã–∫–∞—é—â–µ–≥–æ –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–∞ –≤–ø–ª–æ—Ç—å –¥–æ 100 –∞—Ç—Ç–æ–û–º (0.0000000000000001 –û–º).  –î–∞–ª–µ–µ –Ω–∞—á–∏–Ω–∞—é—Ç—Å—è —á—É–¥–µ—Å–∞, —Å–∫–æ—Ä–µ–µ –≤—Å–µ–≥–æ –≤—ã–∑–≤–∞–Ω–Ω—ã–µ –æ—à–∏–±–∫–∞–º–∏ –æ–∫—Ä—É–≥–ª–µ–Ω–∏—è, –∞ –¥–ª—è –Ω—É–ª–µ–≤–æ–≥–æ —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏—è –ø—Ä–æ–≤–æ–¥–Ω–∏–∫–∞, PSPICE –≤–æ–æ–±—â–µ –æ—Ç–∫–∞–∑—ã–≤–∞–µ—Ç—Å—è —Å—á–∏—Ç–∞—Ç—å. 
_________________
Like the eyes of a cat in the black and blue...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
Artlav

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 22:09:50 |
|
| –ü—Ä–æ—Ä–µ–∑–∞–ª–∏—Å—å –∑—É–±—ã |
 |
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü—Ç –∞–ø—Ä 27, 2012 15:32:24
–°–æ–æ–±—â–µ–Ω–∏–π: 225
–û—Ç–∫—É–¥–∞: –ú–æ—Å–∫–≤–∞
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–ó–≤–µ–∑–¥–æ—á—ë—Ç –ø–∏—Å–∞–ª(–∞): –ø–æ–¥–µ–ª–∏—Ç—å —ç–Ω–µ—Ä–≥–∏—é –ø–æ—Ä–æ–≤–Ω—É –Ω–µ –æ–±–µ—â–∞—é, –∞ –≤–æ—Ç —Å–æ—Ö—Ä–∞–Ω–∏—Ç—å –º–æ–∂–Ω–æ —Ç–∞–∫  –Ý–∞–±–æ—Ç–∞–µ—Ç –≤ —Å–∏–º—É–ª—è—Ç–æ—Ä–µ, –Ω–æ –Ω–µ —Ä–∞–±–æ—Ç–∞–µ—Ç –Ω–∞ –ø—Ä–∞–∫—Ç–∏–∫–µ. –î–≤–∞ –ø–æ 10000uF, –æ–¥–∏–Ω –∑–∞—Ä—è–∂–µ–Ω –Ω–∞ 10–í, –¥–∏–æ–¥, 47000uH –∏–Ω–¥—É–∫—Ç–æ—Ä - –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –¥–µ–ª–∏—Ç—Å—è –ø—Ä–∏–º–µ—Ä–Ω–æ –ø–æ—Ä–æ–≤–Ω—É. –û—Ç —á–µ–≥–æ —Ç–∞–∫?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
El-Eng

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –æ–∫—Ç 26, 2013 22:27:15 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 97
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1584
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 26, 2012 14:44:34
–°–æ–æ–±—â–µ–Ω–∏–π: 3736
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ú–µ–¥–∞–ª–∏: 1

|
Artlav –ø–∏—Å–∞–ª(–∞): –û—Ç —á–µ–≥–æ —Ç–∞–∫? –ò–∑-–∑–∞ –ø–æ—Ç–µ—Ä—å, –Ω–∞–ø—Ä–∏–º–µ—Ä, –Ω–∞ –≤–Ω—É—Ç—Ä–µ–Ω–Ω–µ–º —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏–∏ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç–∏ –∏ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–æ–≤. –î–æ–±–∞–≤—å—Ç–µ –µ–≥–æ –≤ —Å–∏–º—É–ª—è—Ç–æ—Ä (—Å–∫–∞–∂–µ–º, –ø–æ—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª—å–Ω–æ —Å –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å—é) –∏ —É–≤–∏–¥–∏—Ç–µ —Ä–µ–∑—É–ª—å—Ç–∞—Ç.
_________________
Like the eyes of a cat in the black and blue...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
Gudd-Head

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –æ–∫—Ç 27, 2013 11:19:55 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 67
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1065
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —Å–µ–Ω 18, 2008 12:27:21
–°–æ–æ–±—â–µ–Ω–∏–π: 19930
–û—Ç–∫—É–¥–∞: –°—Ç–æ–ª–∏—Ü–∞ –ú–∏—Ä–∞ –°–∞–Ω–∫—Ç-–ü–µ—Ç–µ—Ä–±—É—Ä–≥
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ú–µ–¥–∞–ª–∏: 1

|
|
–ú–æ–∂–µ—Ç –µ—â—ë –¥—Ä–æ—Å—Å–µ–ª—å –Ω–∏–∑–∫–æ—á–∞—Å—Ç–æ—Ç–Ω—ã–π –∏/–∏–ª–∏ –≤—Ö–æ–¥–∏—Ç –≤ –Ω–∞—Å—ã—â–µ–Ω–∏–µ.
_________________
[ –í—Å—ë –¥–µ–ª–æ –Ω–µ —Å—Ç–æ–ª—å–∫–æ –≤ –≤–∞—à–µ–π –≥–ª—É–ø–æ—Å—Ç–∏, —Å–∫–æ–ª—å–∫–æ –≤ –º–æ–µ–π –≥–µ–Ω–∏–∞–ª—å–Ω–æ—Å—Ç–∏ ] [ –ü—Ä–∞–≤–∏–ª—å–Ω–æ –∑–∞–¥–∞–Ω–Ω—ã–π –≤–æ–ø—Ä–æ—Å —Å–æ–¥–µ—Ä–∂–∏—Ç –≤ —Å–µ–±–µ –ø–æ–ª–æ–≤–∏–Ω—É –æ—Ç–≤–µ—Ç–∞ ]
–ò–∑–º–µ—Ä–∏—Ç—å –Ω–Ω–Ω–∞–¥–∞?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
O_l_e_g

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –¥–µ–∫ 28, 2013 01:42:19 |
|
| –ù–∞—à–µ–ª —Ç—Ä–∞–Ω–∑–∏—Å—Ç–æ—Ä. –ü–æ–Ω—é—Ö–∞–ª. |
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –í—Ç –¥–µ–∫ 27, 2011 01:13:21
–°–æ–æ–±—â–µ–Ω–∏–π: 191
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–í–æ—Ç —Ç—É—Ç —è –ø–æ–ø—ã—Ç–∞–ª—Å—è –æ–ø—Ä–µ–¥–µ–ª–∏—Ç—å –∫–∞–∫–æ–µ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –æ—Å—Ç–∞–Ω–µ—Ç—Å—è –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ –µ—Å–ª–∏ —Å –Ω–µ–≥–æ —É–¥–∞–ª–∏—Ç—å –ø–æ–ª–æ–≤–∏–Ω—É –∑–∞—Ä—è–¥–∞. –Ø –ø–æ–º–µ–Ω—è–ª –ø—Ä–µ–¥–µ–ª—ã –∏–Ω—Ç–µ–≥—Ä–∏—Ä–æ–≤–∞–Ω–∏—è –º–µ—Å—Ç–∞–º–∏ —á—Ç–æ–±—ã —Ä–∞–±–æ—Ç–∞ –ø–æ –ø–µ—Ä–µ–º–µ—â–µ–Ω–∏—é –∑–∞—Ä—è–¥–∞ –±—ã–ª–∞ –ø–æ–ª–æ–∂–∏—Ç–µ–ª—å–Ω—ã (–¥–ª—è —É–¥–æ–±—Å—Ç–≤–∞) –∑–Ω–∞–∫ –ø—Ä–æ—Å—Ç–æ –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç –∑–∞ —Å—á–µ—Ç —á–µ–≥–æ —Å–æ–≤–µ—Ä—à–∞–µ—Ç—Å—è —Ä–∞–±–æ—Ç–∞ (—ç–Ω–µ—Ä–≥–∏—è —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–≥–æ –ø–æ–ª—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ –∏–ª–∏ –≤–Ω–µ—à–Ω–µ–µ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–µ –ø–æ–ª–µ. –ü–æ–Ω—è—Ç–Ω–æ —á—Ç–æ –ø—Ä–∏ —Ä–∞–∑—Ä—è–¥–µ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ —Ä–∞–±–æ—Ç—É —Å–æ–≤–µ—Ä—à–∞–µ—Ç —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–µ –ø–æ–ª–µ —Å–∞–º–æ–≥–æ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞. –¢–∞–∫ –≤–æ—Ç —á—Ç–æ –ø–æ–ª—É—á–∏–ª–æ—Å—å –°–ø–æ–π–ª–µ—Ä –¢–æ –µ—Å—Ç—å –µ—Å–ª–∏ "—É–¥–∞–ª–∏—Ç—å" —Å –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ 0,5 –∑–∞—Ä—è–¥–∞ —Ç–æ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –Ω–∞ –Ω–µ–º —Å—Ç–∞–Ω–µ—Ç 0,707 –æ—Ç –ø–µ—Ä–≤–æ–Ω–∞—á–∞–ª—å–Ω–æ–≥–æ, —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤–µ–Ω–Ω–æ –µ—Å–ª–∏ –ø–æ–º–µ—Å—Ç–∏—Ç—å –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä 0,5 –∑–∞—Ä—è–¥–∞ —Ç–æ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –Ω–∞ –Ω–µ–º —Å—Ç–∞–Ω–µ—Ç 0,707 –æ—Ç –º–∞–∫—Å–∏–º–∞–ª—å–Ω–æ–≥–æ (–∫–æ—Ç–æ—Ä–æ–µ —Å—Ç–∞–ª–æ –±—ã –Ω–∞ –Ω–µ–º –µ—Å–ª–∏ –ø–æ–º–µ—Å—Ç–∏—Ç—å –Ω–∞ –∫–æ–Ω–¥–µ—Ä –≤–µ—Å—å –∑–∞—Ä—è–¥). –í –¥–∞–Ω–Ω–æ–º —Å–ª—É—á–∞–µ —Å–æ—Ö—Ä–∞–Ω—è–µ—Ç—Å—è –∑–∞–∫–æ–Ω —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è —ç–Ω–µ—Ä–≥–∏–∏ –∏ –∑–∞—Ä—è–¥–∞. –í–æ–∑–Ω–∏–∫–∞–µ—Ç –≤–æ–ø—Ä–æ—Å —Å –µ–º–∫–æ—Å—Ç—å—é. –ù–æ –µ—Å–ª–∏ –µ–º–∫–æ—Å—Ç—å –≤ –¥–∞–Ω–Ω–æ–º —Å–ª—É—á–∞–µ —Ä–∞—Å—Å–º–∞—Ç—Ä–∏–≤–∞—Ç—å –Ω–µ –∫–∞–∫ "–≥–µ–æ–º–µ—Ç—Ä–∏—á–µ—Å–∫—É—é –≤–µ–ª–∏—á–∏–Ω—É" –∞ –∫–∞–∫ "–∫–æ–ª–∏—á–µ—Å—Ç–≤–æ —É—Å–ª–æ–≤–Ω–æ–≥–æ —Ç–æ–ø–ª–∏–≤–∞ –≤ —Å–∏—Å—Ç–µ–º–µ", —Ç–æ –≤—Å–µ —Å—Ç–∞–Ω–æ–≤–∏—Ç—å—Å—è –Ω–∞ —Å–≤–æ–∏ –º–µ—Å—Ç–∞. –î–æ –Ω–∞—á–∞–ª–∞ —Ä–∞–∑—Ä—è–¥–∞ –µ–º–∫–æ—Å—Ç—å –±—ã–ª–∞ –º–∞–∫—Å–∏–º–∞–ª—å–Ω–∞ –∏ —Ä–∞–≤–Ω–∞ –°, –æ—Ç–æ–±—Ä–∞–ª–∏ 0,5 –∑–∞—Ä—è–¥–∞ –∏ –∑–∞–ø–∞—Å —É—Å–ª–æ–≤–Ω–æ–≥–æ —Ç–æ–ø–ª–∏–≤–∞ —É–º–µ–Ω—å—à–∏–ª—Å—è –≤ –¥–∞–Ω–Ω–æ–º —Å–ª—É—á–∞–µ –¥–æ 0,707 –æ—Ç –ø–µ—Ä–≤–æ–Ω–∞—á–∞–ª—å–Ω–æ–≥–æ. –î–∞–Ω–Ω—ã–π –ø–æ–¥—Ö–æ–¥ –ø–æ–∑–≤–æ–ª—è–µ—Ç –∏–∑–±–µ–∂–∞—Ç—å —É—á–∏—Ç—ã–≤–∞—Ç—å —Ä–∞–∑–ª–∏—á–Ω—ã–µ –ø–æ—Ç–µ—Ä–∏ —ç–Ω–µ—Ä–≥–∏–∏ –ø—Ä–∏ –ø–µ—Ä–µ–∑–∞—Ä—è–¥–∫–µ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–æ–≤. –ê —Ç–∞–∫–∂–µ –ø–æ–∫–∞–∑—ã–≤–∞–µ—Ç —á—Ç–æ –ø—Ä–∏ —Ä–∞–∑—Ä—è–¥–∫–µ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ —Å–∞–º–æ–≥–æ –Ω–∞ —Å–µ–±—è –∫–æ–ª–µ–±—è–Ω–∏—è –Ω–µ –≤–æ–∑–Ω–∏–∫–Ω—É—Ç (—Ç–∞–∫ –∫–∞–∫ –¥–ª—è –ø–µ—Ä–≤–æ–≥–æ –¥–∏—Ñ—Ñ–µ—Ä–µ–Ω—Ü–∏–∞–ª—å–Ω–æ–≥–æ —É—Ä–∞–≤–Ω–µ–Ω–∏—è, —á—Ç–æ —è –≤—ã—á–∏—Å–ª—è–ª, –Ω–µ—Ç —Ä–µ—à–µ–Ω–∏–π –≤ –≤–∏–¥–µ –ø–µ—Ä–∏–æ–¥–∏—á–µ—Å–∫–∏—Ö —Ñ—É–Ω–∫—Ü–∏–π), –≤ –∫–æ–Ω—Ü–µ —Ä–∞–∑—Ä—è–¥–∫–∏ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –±—É–¥–µ—Ç 0. –ê –≤—Å—è —ç–Ω–µ—Ä–≥–∏—è —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–≥–æ –ø–æ–ª—è –ø–æ–π–¥–µ—Ç –Ω–∞ –ø–µ—Ä–µ–º–µ—â–µ–Ω–∏–µ –Ω–∞–∫–æ–ø–ª–µ–Ω–Ω–æ–≥–æ –∑–∞—Ä—è–¥–∞ —Å –æ–¥–Ω–æ–π –æ–±–∫–ª–∞–¥–∫–∏ –Ω–∞ –¥—Ä—É–≥—É—é –∏ –≤—ã—Ä–∞–≤–Ω–∏–≤–∞–Ω–∏—è –ø–æ—Ç–µ–Ω—Ü–∏–∞–ª–æ–≤.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
rl55

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –¥–µ–∫ 28, 2013 04:41:45 |
|
–ö–∞—Ä–º–∞: 79
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1412
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä —Ñ–µ–≤ 13, 2013 21:59:40
–°–æ–æ–±—â–µ–Ω–∏–π: 16166
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
O_l_e_g –ø–∏—Å–∞–ª(–∞): –¢–æ –µ—Å—Ç—å –µ—Å–ª–∏ "—É–¥–∞–ª–∏—Ç—å" —Å –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ 0,5 –∑–∞—Ä—è–¥–∞ —Ç–æ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –Ω–∞ –Ω–µ–º —Å—Ç–∞–Ω–µ—Ç 0,707 –æ—Ç –ø–µ—Ä–≤–æ–Ω–∞—á–∞–ª—å–Ω–æ–≥–æ –ê –∫–∞–∫ –∂–µ c —Ñ–æ—Ä–º—É–ª–æ–π U=q/C? –ï—Å–ª–∏ –∑–∞—Ä—è–¥ —Å—Ç–∞–ª 0,5q, —Ç–æ –∏ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –¥–æ–ª–∂–Ω–æ —Å—Ç–∞—Ç—å 0,5U. –í–æ—Ç –≤—ã –ø—Ä–∞–≤–∏–ª—å–Ω–æ –ø–æ—Å—á–∏—Ç–∞–ª–∏, —á—Ç–æ –µ—Å–ª–∏ —É–º–µ–Ω—å—à–∏—Ç—å –∑–∞—Ä—è–¥ –Ω–∞ 0,5q, —Ç–æ —ç–Ω–µ—Ä–≥–∏—è –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ –±—É–¥–µ—Ç —Ä–∞–≤–Ω–∞ 0,25(CU^2)/2. –ù–æ –¥–∞–ª–µ–µ, –ø–æ—á–µ–º—É –≤—ã –ø—Ä–∏—Ä–∞–≤–Ω–∏–≤–∞–µ—Ç–µ –Ω–∞—á–∞–ª—å–Ω—É—é —ç–Ω–µ—Ä–≥–∏—é —Å —ç–Ω–µ—Ä–≥–∏–µ–π –ø–æ—Å–ª–µ —É–¥–∞–ª–µ–Ω–∏—è 0,5 –∑–∞—Ä—è–¥–∞?  –ù—É –∏ –¥–∞–ª—å—à–µ –ø—Ä–æ—Å—Ç–æ —Å–æ–≤–µ—Ä—à–∞–µ—Ç–µ –æ—à–∏–±–∫—É –≤ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω–Ω–æ–º –≤—ã—á–∏—Å–ª–µ–Ω–∏–∏ U2    –ù–µ–ø–æ–Ω—è—Ç–Ω–æ —Ç–æ–ª—å–∫–æ, –∫–∞–∫ —á–µ–ª–æ–≤–µ–∫ –º–æ–∂–µ—Ç –≤—ã—á–∏—Å–ª—è—Ç—å –∏–Ω—Ç–µ–≥—Ä–∞–ª—ã, –¥–æ–ø—É—Å–∫–∞—è —Ç–∞–∫–∏–µ –æ—à–∏–±–∫–∏... –ï—Å–ª–∏ –≤—Å–ø–æ–º–Ω–∏—Ç—å —à–∫–æ–ª—É, —Ç–æ U2=2U1, —á—Ç–æ –µ—Å—Ç—å –ø–æ–ª–Ω–∞—è —á—É—à—å. –ê —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω–æ –¥–æ–ª–∂–Ω–æ –∏–∑ —Ñ–æ—Ä–º—É–ª—ã U=q/C –ø–æ–ª—É—á–∏—Ç—å—Å—è U2=0.5U1. –¢–∞–∫–∂–µ –Ω–µ–±–µ–∑–∏–Ω—Ç–µ—Ä–µ—Å–Ω–æ, —á—Ç–æ –≤—Ç–æ—Ä–æ–π –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä –ø—Ä–∏ —ç—Ç–æ–º –ø–æ–ª—É—á–∏—Ç —ç–Ω–µ—Ä–≥–∏—é 0,75(CU^2)/2 –û—Ç—Å—é–¥–∞ –Ω–∞ –≤—Ç–æ—Ä–æ–º –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ –¥–æ–ª–∂–Ω–æ –±—ã—Ç—å –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ (sqrt 0,75)U=0,866U. –ê —ç—Ç–æ —Å—Ç–∞—Ü–∏–æ–Ω–∞—Ä–Ω–æ –Ω–∏–∫–∞–∫ –Ω–µ –º–æ–∂–µ—Ç –±—ã—Ç—å, —Ç.–∫. –Ω–∞ –ø–µ—Ä–≤–æ–º –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ 0,5U. –¢–∞–∫ –≤–æ—Ç, –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –ø–æ 0.707U –±—É–¥–µ—Ç, –µ—Å–ª–∏ —ç–Ω–µ—Ä–≥–∏—é –ø–æ–¥–µ–ª–∏—Ç—å –º–µ–∂–¥—É –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞–º–∏ –ø–æ—Ä–æ–≤–Ω—É. –¢–æ–ª—å–∫–æ –∑–∞—Ä—è–¥—ã –Ω–∞ –Ω–∏—Ö –±—É–¥—É—Ç –Ω–µ –ø–æ 0,5q, –∞ –ø–æ 0,707q, –∫–∞–∫ —ç—Ç–æ –Ω–∏ –ø–∞—Ä–∞–¥–æ–∫—Å–∞–ª—å–Ω–æ... –ê –∫–∞–∫ –ø–æ–¥–µ–ª–∏—Ç—å —ç–Ω–µ—Ä–≥–∏—é, –±—ã–ª–æ –æ–ø–∏—Å–∞–Ω–æ —á—É—Ç—å —Ä–∞–Ω–µ–µ.
| –í–ª–æ–∂–µ–Ω–∏—è: |
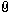 26.JPG [5.82 KiB]
26.JPG [5.82 KiB]
–°–∫–∞—á–∏–≤–∞–Ω–∏–π: 1027
|
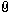 25.JPG [2.27 KiB]
25.JPG [2.27 KiB]
–°–∫–∞—á–∏–≤–∞–Ω–∏–π: 1173
|
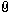 24.JPG [3.05 KiB]
24.JPG [3.05 KiB]
–°–∫–∞—á–∏–≤–∞–Ω–∏–π: 1201
|
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
O_l_e_g

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –¥–µ–∫ 28, 2013 18:21:38 |
|
| –ù–∞—à–µ–ª —Ç—Ä–∞–Ω–∑–∏—Å—Ç–æ—Ä. –ü–æ–Ω—é—Ö–∞–ª. |
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –í—Ç –¥–µ–∫ 27, 2011 01:13:21
–°–æ–æ–±—â–µ–Ω–∏–π: 191
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
rl55
–ù—É –ø–µ—Ä–µ–ø—É—Ç–∞–ª –∏–Ω–¥–µ–∫—Å—ã —Ç–∞–∫ –∫–∞–∫ –≤ –≤–æ—Ä–¥–µ —Å–ª–æ–∂–Ω–æ —Ñ–æ—Ä–º—É–ª—ã –Ω–∞–±–∞—Ä–∞—Ç—å –≤–æ—Ç –∏ –ø—Ä–∏—Ö–æ–¥–∏—Ç—å—Å—è –¥–µ–ª–∞—Ç—å –∫–æ–ø–∏—Ä–æ–≤–∞–Ω–∏–µ —Å –ø–æ—Å–ª–µ–¥—É—â–µ–π –º–æ–¥–∏—Ñ–∏–∫–∞—Ü–∏–µ–π.
–û—á–µ–≤–∏–¥–Ω–æ –∂–µ —á—Ç–æ –ø–æ—Å–ª–µ —Ä–∞–∑—Ä—è–¥–∞ –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ –æ—Å—Ç–∞–ª–æ—Å—å 0,25 –æ—Ç –ø–µ—Ä–≤–æ–Ω–∞—á–∞–ª—å–Ω–æ–π —ç–Ω–µ—Ä–≥–∏–∏
–ê1=0,25*–°*U1*U1/2
–∫–∞–∫–æ–º—É –Ω–æ–≤–æ–º—É –Ω–∞–ø—Ä—è–∂–µ–Ω–∏—é U2 –±—É–¥–µ—Ç —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤–æ–≤–∞—Ç—å —ç—Ç–æ –Ω–æ–≤–æ–µ –∑–Ω–∞—á–µ–Ω–∏–µ —ç–Ω–µ—Ä–≥–∏–∏, –≤—Å–µ –æ—á–µ–Ω—å –ø—Ä–æ—Å—Ç–æ
A1=C*U2*U2/2
–ø—Ä–∏—Ä–∞–≤–Ω—è–µ–º –ø—Ä–∞–≤—ã–µ —á–∞—Å—Ç–∏ –∏ –ø–æ–ª—É—á–∏–º
C*U2*U2/2=0,25*–°*U1*U1/2
–ø–æ—Å–ª–µ —É–ø—Ä–æ—â–µ–Ω–∏—è –ø–æ–ª—É—á–∞–µ–º
U2*U2=0.25*U1*U1
–æ—Ç—Å—é–¥–∞ –∏ –ø–æ–ª—É—á–∏–ª–æ—Å—å U2=0.707*U1
–≤—Å–µ –æ—á–µ–≤–∏–¥–Ω–æ –µ—Å–ª–∏ —Ä–µ—à–∏—Ç—å –¥–∏—Ñ —É—Ä–∞–≤–Ω–µ–Ω–∏–µ. –î–µ–ª–æ –≤ —Ç–æ–º —á—Ç–æ —Ä–∞–±–æ—Ç–∞ –∑–∞—Ç—Ä–∞—á–∏–≤–∞–µ–º–∞—è –Ω–∞ –ø–µ—Ä–µ–º–µ—â–µ–Ω–∏—è –∑–∞—Ä—è–¥–∞ –≤ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–º –ø–æ–ª–µ A=E*q –Ω–æ –ø—Ä–∏ —É–º–µ–Ω—å—à–µ–Ω–∏–∏ –∑–∞—Ä—è–¥–∞ —É–º–µ–Ω—å—à–∞–µ—Ç—Å—è –∏ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –Ω–∞ –æ–±–∫–ª–∞–¥–∫–∞—Ö –∑–∞—Ä—è–¥–∞. –ê —ç—Ç–æ –∑–Ω–∞—á–∏—Ç –¥–ª—è –ø–µ—Ä–µ–º–µ—â–µ–Ω–∏—è –∫–∞–∂–¥–æ–π —Å–ª–µ–¥—É—é—â–µ–π –ø–æ—Ä—Ü–∏–∏ –∑–∞—Ä—è–¥–∞ —Ç—Ä–µ–±—É–µ—Ç—Å—è –≤—Å–µ –º–µ–Ω—å—à–µ —ç–Ω–µ—Ä–≥–∏–∏. –ò–º–µ–Ω–Ω–æ –ø–æ—ç—Ç–æ–º—É –Ω–∏–∫–∞–∫–∏—Ö –∫–æ–ª–µ–±–∞–Ω–∏–π –Ω–∏–∫–æ–≥–¥–∞ –∏ –Ω–µ –±—É–¥–µ—Ç –≤–æ–∑–Ω–∏–∫–∞—Ç—å. –¢–∞–∫ –∫–∞–∫ "—Å –ø–æ–∫–∏–¥–∞–Ω–∏–µ–º –ø–æ—Å–ª–µ–¥–Ω–µ–≥–æ —ç–ª–µ–∫—Ç—Ä–æ–Ω–∞" –∏ —Ä–µ–∑—É–ª—å—Ç–∏—Ä—É—é—â–µ–µ –ø–æ–ª–µ —Å—Ç–∞–Ω–µ—Ç —Ä–∞–≤–Ω—ã–º 0. –ê —ç—Ç–æ –∑–Ω–∞—á–∏—Ç –Ω–µ—Ç –Ω–∏–∫–∞–∫–∏—Ö –≤–Ω–µ—à–Ω–∏—Ö —Å–∏–ª —á—Ç–æ–±—ã –∑–∞—Å—Ç–∞–≤–∏—Ç—å –Ω–∞—á–∞—Ç—å –ø–µ—Ä–µ–∑–∞—Ä—è–∂–∞—Ç—å—Å—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä. –ö–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä –ø—Ä–æ—Å—Ç–æ —Ä–∞–∑—Ä—è–¥–∏—Ç—Å—è –ø–æ —ç–∫—Å–ø–æ–Ω–µ–Ω—Ç–µ –∏ –∑–∞—Ä—è–¥—ã —É—Ä–∞–≤–Ω–æ–≤–µ—Å—è—Ç—å—Å—è. –ï—Å–ª–∏ –¥–æ–±–∞–≤–∏—Ç–µ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç—å –≤ –∑–∞–¥–∞—á—É —Ç–æ —Ä–µ—à–µ–Ω–∏–µ –±—É–¥–µ—Ç —Å–æ–≤–µ—Ä—à–µ–Ω–Ω–æ –¥—Ä—É–≥–∏–º. –£–ø—Ä—É–≥–∏–µ —Å–≤–æ–π—Å—Ç–≤–∞ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã—Ö —á–∞—Å—Ç–∏—Ü –∏ –∫–≤–∞–Ω—Ç–æ–≤—ã–µ —ç—Ñ—Ñ–µ–∫—Ç—ã –ø—Ä–∏–º–µ–Ω—è—Ç—å –Ω–µ –±—É–¥–µ–º –∫–ª–∞—Å—Å–∏—á–µ—Å–∫–∞—è —ç–ª–µ–∫—Ç—Ä–æ—Ç–µ—Ö–Ω–∏–∫–∞ –Ω–µ –∏—Å–ø–æ–ª—å–∑—É–µ—Ç —Ç–∞–∫–∏–µ –ø–æ–Ω—è—Ç–∏—è –Ω–æ —ç—Ç–æ –Ω–µ –∑–Ω–∞—á–∏—Ç —á—Ç–æ —ç–ª–µ–∫—Ç—Ä–æ—Ç–µ—Ö–Ω–∏–∫–∞ –ø—Ä–æ—Ç–∏–≤–æ—Ä–µ—á–∏–≤–∞. –ü—Ä–æ—Å—Ç–æ —Å—É—â–µ—Å—Ç–≤—É—é—Ç –≥—Ä–∞–Ω–∏—Ü—ã –≤ –∫–æ—Ç–æ—Ä—ã—Ö —Ä–µ–∑—É–ª—å—Ç–∞—Ç —Å–æ–≥–ª–∞—Å—É–µ—Ç—Å—è —Å –æ–ø—ã—Ç–æ–º - —ç—Ç–æ –∏ –µ—Å—Ç—å –≥—Ä–∞–Ω–∏—Ü—ã –ø—Ä–∏–º–µ–Ω–∏–º–æ—Å—Ç–∏. –¢–∞–∫ —á—Ç–æ –æ–ø–∏—Å–∞—Ç—å –ø—Ä–æ—Ü–µ—Å—Å –∑–∞—Ä—è–¥–∞ —Ä–∞–∑—Ä—è–¥–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ —ç–ª–µ–∫—Ç—Ä–æ—Ç–µ—Ö–Ω–∏–∫–∞ –º–æ–∂–µ—Ç. –ê –≤–æ—Ç –∏—Å–ø–æ–ª—å–∑–æ–≤–∞—Ç—å –µ–µ –¥–ª—è –æ–ø–∏—Å–∞–Ω–∏—è —Ä–∞–±–æ—Ç—ã –∞—Ç–æ–º–Ω–æ–≥–æ –∫–æ–ª–∞–π–¥–µ—Ä–∞ –≤–µ—Ä–æ—è—Ç–Ω–æ —É–∂–µ –Ω–µ–ª—å–∑—è.
–ï—â–µ —Ä–∞–∑ –ø–æ–≤—Ç–æ—Ä—é—Å—å. –ü—Ä–∏ —Ä–∞–∑—Ä—è–¥–∫–µ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ —É–º–µ–Ω—å—à–∞–µ—Ç—Å—è –∑–∞—Ä—è–¥ –∞ –∑–Ω–∞—á–∏—Ç –∏ —Ä–µ–∑—É–ª—å—Ç–∏—Ä—É—é—â–∞—è —Å–∏–ª–∞ –¥–µ–π—Å—Ç–≤—É—é—â–∞—è –Ω–∞ –æ—Å—Ç–∞–≤—à–∏–µ—Å—è –∑–∞—Ä—è–¥—ã. –¢–∞–∫–æ–µ —Ä–µ—à–µ–Ω–∏–µ –Ω–∞–¥–æ –∏—Å–∫–∞—Ç—å –∏—Å–∫–ª—é—á–∏—Ç–µ–ª—å–Ω–æ –≤ –≤–∏–¥–µ –¥–∏—Ñ —É—Ä–∞–≤–Ω–µ–Ω–∏—è.
–ö–æ–Ω–µ—á–Ω—ã–π —Ä–µ–∑—É–ª—å—Ç–∞—Ç –µ—Å–ª–∏ –≤—ã —Ä–µ—à–∏—Ç–µ —É—Ä–∞–≤–Ω–µ–Ω–∏–µ –∫–æ–≥–¥–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä –ø–æ–ª–Ω–æ—Å—Ç—å—é —Ä–∞–∑—Ä—è–¥–∏—Ç—å—Å—è –Ω–µ –±—É–¥–µ—Ç –ø—Ä–æ—Ç–∏–≤–æ—Ä–µ—á–∏—Ç—å –≤–∞—à–µ–π —Ñ–æ—Ä–º—É–ª–µ
U=q/C'
–ê –≤–æ—Ç —á—Ç–æ —Å–æ–±–æ–π –ø—Ä–µ–¥—Å—Ç–∞–≤–ª—è–µ—Ç –∫–æ—ç—Ñ –ø—Ä–æ–ø–æ—Ä—Ü–∏–æ–Ω–∞–ª—å–Ω–æ—Å—Ç–∏ –° –º–µ–∂–¥—É –∑–∞—Ä—è–¥–æ–º –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ –∏ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ–º –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ –Ω–∞–¥–æ –µ—â–µ —Ä–∞–∑–±–∏—Ä–∞—Ç—å—Å—è –ò —Ä–∞–≤–µ–Ω –ª–∏ –æ–Ω –µ–º–∫–æ—Å—Ç–∏ –≤ –Ω–∞—à–µ–º –ø–æ–Ω–∏–º–∞–Ω–∏–µ –æ–±–æ–∑–Ω–∞—á–∏–º –µ–µ –°'. –°–µ–π—á–∞—Å —è –Ω–µ –º–æ–≥—É –æ—Ç–≤–µ—Ç–∏—Ç—å –Ω–∞ —ç—Ç–æ—Ç –≤–æ–ø—Ä–æ—Å. –ü—Ä–∏ —Ä–µ—à–µ–Ω–∏–∏ –¥–∏—Ñ —É—Ä–∞–≤–Ω–µ–Ω–∏—è —è –∏—Å–ø–æ–ª—å–∑–æ–≤–∞–ª –ø–æ—Å—Ç–æ—è–Ω–Ω—É—é –æ–±–æ–∑–Ω–∞—á–∏–≤ –µ–µ –∫–∞–∫ –°. –¢–∞–∫–æ–π –ø–æ–¥—Ö–æ–¥ –ø—Ä–∞–≤–æ–º–µ—Ä–µ–Ω —Ç–∞–∫ –∫–∞–∫ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–µ –ø–æ–ª–µ –ø–æ—Ç–µ–Ω—Ü–∏–∞–ª—å–Ω–æ, –∞ —ç—Ç–æ –∑–Ω–∞—á–∏—Ç –º–µ–∂–¥—É —Ä–∞–±–æ—Ç–æ–π —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–∏–º –ø–æ–ª–µ–º –∏ –∑–∞—Ä—è–¥–æ–º –∏–º–µ–µ—Ç—Å—è –ª–∏–Ω–µ–π–Ω–∞—è –∑–∞–≤–∏—Å–∏–º–æ—Å—Ç—å –∏ –ø—Ä–∞–≤–∏–ª—å–Ω—ã–º –≤—ã–±–æ—Ä–æ–º –µ–¥–∏–Ω–∏—Ü –∏–∑–º–µ—Ä–µ–Ω–∏—è –º–æ–∂–Ω–æ –≤–æ–æ–±—â–µ —Å–¥–µ–ª–∞—Ç—å –¥–∞–Ω–Ω—ã–π –∫–æ—ç—Ñ –ø—Ä–æ–ø–æ—Ä—Ü–∏–æ–Ω–∞–ª—å–Ω–æ—Å—Ç–∏ —Ä–∞–≤–Ω—ã–º 1. –í —Å–∏—Å—Ç–µ–º–µ –°–ò —ç—Ç–æ—Ç –∫–æ—ç—Ñ –ø—Ä–æ–ø–æ—Ä—Ü–∏–æ–Ω–∞–ª—å–Ω–æ—Å—Ç–∏ –∏–º–µ–µ—Ç —Ä–∞–∑–º–µ—Ä–Ω–æ—Å—Ç—å –§–∞—Ä–∞–¥—ã.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
Microwatt

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –¥–µ–∫ 28, 2013 18:59:32 |
|
–ö–∞—Ä–º–∞: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 5
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä –∞–≤–≥ 24, 2011 23:53:51
–°–æ–æ–±—â–µ–Ω–∏–π: 718
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
Vendein_RaZoR –ø–∏—Å–∞–ª(–∞): –ò–º–µ–µ–º —Ç–∞–∫—É—é –∑–∞–¥–∞—á—É : –¶–∏—Ç–∞—Ç–∞: –ü–æ –∑–∞–∫–æ–Ω—É —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è –∑–∞—Ä—è–¥–∞ –≤ –∫–∞–∂–¥–æ–º –∏–∑ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–æ–≤ –æ–∫–∞–∂–µ—Ç—Å—è –ø–æ –ø–æ–ª–æ–≤–∏–Ω–µ –∏—Å—Ö–æ–¥–Ω–æ–≥–æ –∑–∞—Ä—è–¥–∞, —Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª—å–Ω–æ –Ω–∞–ø—Ä—è–∂–µ–Ω–∏–µ –ø–æ—Å–ª–µ –ø–æ–¥–∫–ª—é—á–µ–Ω–∏—è –≤—Ç–æ—Ä–æ–≥–æ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ —Å—Ç–∞–Ω–µ—Ç —Ä–∞–≤–Ω—ã–º –ø–æ–ª–æ–≤–∏–Ω–µ –∏—Å—Ö–æ–¥–Ω–æ–≥–æ: U=Q/2C. –¢–µ–ø–µ—Ä—å —Å—á–∏—Ç–∞–µ–º —ç–Ω–µ—Ä–≥–∏—é –≤ –ø–æ–ª—É—á–∏–≤—à–µ–π—Å—è —Å–∏—Å—Ç–µ–º–µ: 2*C*(U/2)^2/2=CU^2/4 —á—Ç–æ –≤ –¥–≤–∞ —Ä–∞–∑–∞ –º–µ–Ω—å—à–µ –∏—Å—Ö–æ–¥–Ω–æ–π —ç–Ω–µ—Ä–≥–∏–∏.
–ö—É–¥–∞ –¥–µ–ª–∞—Å—å –ø–æ–ª–æ–≤–∏–Ω–∞ –∑–∞–ø–∞—Å—ë–Ω–Ω–æ–π –≤ –æ–¥–Ω–æ–º –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ —ç–Ω–µ—Ä–≥–∏–∏?  —à—Å—Ç—å —Å—Ç—Ä–∞–Ω–∏—Ü –æ–±—Å—É–∂–¥–µ–Ω–∏—è –Ω–µ–ª–µ–ø–æ—Å—Ç–∏. –í —É—Å–ª–æ–≤–∏–∏ –∑–∞–¥–∞—á–∏ –≥—Ä—É–±–∞—è –æ—à–∏–±–∫–∞. –ù–∞–ø—Ä—è–∂–µ–Ω–∏–µ –Ω–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞—Ö –±—É–¥–µ—Ç –Ω–µ 0.5 –∏—Å—Ö–æ–¥–Ω–ª–≥–æ , –∞ –∫–æ—Ä–µ–Ω—å –∏–∑ 0.5, —Ç.–µ. 0.707. –≠—Ç–æ –≤—ã—Ç–µ–∫–∞–µ—Ç –∏–∑ –∑–∞–∫–æ–Ω–∞ —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è —ç–Ω–µ—Ä–≥–∏–∏. –î–æ—Å—Ç–∞—Ç–æ—á–Ω–æ –ø—Ä–æ—Å—Ç–æ–π –∞–ª–≥–µ–±—Ä—ã, –±–µ–∑ –∏–Ω—Ç–µ–≥—Ä–∞–ª–æ–≤. –°U1^2=2CU2^2 –ü–æ–ª–∞–≥–∞—è –°=1, U1=1, —Ä–µ—à–∞–µ–º –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ U2. –ü–æ–ø—ã—Ç–∫–∏ —Ä–µ–∞–ª—å–Ω–æ–≥–æ –º–æ–¥–µ–ª–∏—Ä–æ–≤–∞–Ω–∏—è –Ω–µ–∫–æ—Ä—Ä–µ–∫—Ç–Ω—ã, —Ç–∞–º —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏–µ —Ü–µ–ø–∏ –¥–æ–ª–∂–Ω–æ —É—á–∞—Å—Ç–≤–æ–≤–∞—Ç—å, —á–∞—Å—Ç—å —ç–Ω–µ—Ä–≥–∏–∏ –ø–æ—Ç–µ—Ä—è–µ—Ç—Å—è –Ω–∞ –Ω–µ–º. –í –æ–±—â–µ–º, —Å–∞–º–∞ –∑–∞–¥–∞—á–∞ –∏–∑ –æ–±–ª–∞—Å—Ç–∏ —Å—Ö–æ–ª–∞—Å—Ç–∏–∫–∏, —Å–∞–º –ø—Ä–æ—Ü–µ—Å—Å —Ä–∞–∑—Ä—è–¥–∞ –∏–¥–µ–∞–ª—å–Ω–æ–π –µ–º–µ–æ—Å—Ç–∏ –Ω–∞ –∏–¥–µ–∞–ª—å–Ω—É—é –µ–º–∫–æ—Å—Ç—å —Ñ–∏–∑–∏—á–µ—Å–∫–∏ –Ω–µ—Ä–µ–∞–ª–∏–∑—É–µ–º. –Ω–µ —Å—É—â–µ—Å—Ç–≤—É–µ—Ç —Ç–∞–∫–∏—Ö –µ–º–∫–æ—Å—Ç–µ–π.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
Stalker007

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –¥–µ–∫ 28, 2013 19:17:15 |
|
| –ì–æ–≤–æ—Ä—è—â–∏–π —Å —Ç–µ–∫—Å—Ç–æ–ª–∏—Ç–æ–º |
 |
–ö–∞—Ä–º–∞: 3
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 38
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä —Å–µ–Ω 08, 2010 20:33:39
–°–æ–æ–±—â–µ–Ω–∏–π: 1502
–û—Ç–∫—É–¥–∞: –í–æ—Ä–æ–Ω–µ–∂
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
Microwatt –ø–∏—Å–∞–ª(–∞): –≠—Ç–æ –≤—ã—Ç–µ–∫–∞–µ—Ç –∏–∑ –∑–∞–∫–æ–Ω–∞ —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è —ç–Ω–µ—Ä–≥–∏–∏. –ê –ø—Ä–æ –∑–∞–∫–æ–Ω —Å–æ—Ö—Ä–∞–Ω–µ–Ω–∏—è –∑–∞—Ä—è–¥–∞ –Ω–µ —Å–ª—ã—Ö–∞–ª–∏?
_________________
–° —à–µ—Ä—Å—Ç—å—é –Ω–∞ —Å–∞–π—Ç–µ –ø–æ—Å—Ç–æ—è–Ω–Ω—ã–µ –ø—Ä–æ–±–ª–µ–º—ã. –û–±–µ—â–∞–ª–∏ –∏—Å–ø—Ä–∞–≤–∏—Ç—å, –Ω–æ –Ω–∏–∫–∞–∫. –í–æ—Ç —Ä–∞–±–æ—Ç–∞—é—â–∞—è —Å—Å—ã–ª–∫–∞, –µ—Å–ª–∏ –∫–æ–º—É –Ω—É–∂–Ω–æ. http://radiokot.ru/circuit/power/charger/40/
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
vem566

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ö—É–¥–∞ –¥–µ–≤–∞–µ—Ç—Å—è —ç–Ω–µ—Ä–≥–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ ?  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –¥–µ–∫ 28, 2013 19:19:18 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 40
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 613
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –í—Å —è–Ω–≤ 24, 2010 13:14:02
–°–æ–æ–±—â–µ–Ω–∏–π: 4713
–û—Ç–∫—É–¥–∞: –û–º—Å–∫
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
Microwatt, –º–æ–∂–Ω–æ –≤–µ—Ä–Ω—É—Ç—å—Å—è –∫ –ø–µ—Ä–≤–æ–π —Å—Ç—Ä–∞–Ω–∏—Ü–µ. –í –ø–µ—Ä–≤–æ–º –æ—Ç–≤–µ—Ç–µ —è –ø–∏—Å–∞–ª vem566 –ø–∏—Å–∞–ª(–∞): –í —Å–≤–æ–µ –≤—Ä–µ–º—è –ø–æ–ø–∞–ª–∞—Å—å –∫–Ω–∏–∂–∫–∞ "–°–æ—Ñ–∏—Å—Ç–∏–∫–∞ –≤ —Ñ–∏–∑–∏–∫–µ", –æ—Ç—Ç—É–¥–∞? –í –ø—É—Å—Ç—É—é —Å—Ç–æ–ª—å–∫–æ —É—Å–∏–ª–∏–π.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
 
|
–°—Ç—Ä–∞–Ω–∏—Ü–∞ 8 –∏–∑ 29
|
[ –°–æ–æ–±—â–µ–Ω–∏–π: 564 ] |
... , , , , , , ... |
–ö—Ç–æ —Å–µ–π—á–∞—Å –Ω–∞ —Ñ–æ—Ä—É–º–µ |
–°–µ–π—á–∞—Å —ç—Ç–æ—Ç —Ñ–æ—Ä—É–º –ø—Ä–æ—Å–º–∞—Ç—Ä–∏–≤–∞—é—Ç: –Ω–µ—Ç –∑–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω–Ω—ã—Ö –ø–æ–ª—å–∑–æ–≤–∞—Ç–µ–ª–µ–π –∏ –≥–æ—Å—Ç–∏: 27 |
|
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –Ω–∞—á–∏–Ω–∞—Ç—å —Ç–µ–º—ã
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –æ—Ç–≤–µ—á–∞—Ç—å –Ω–∞ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ —Ä–µ–¥–∞–∫—Ç–∏—Ä–æ–≤–∞—Ç—å —Å–≤–æ–∏ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ —É–¥–∞–ª—è—Ç—å —Å–≤–æ–∏ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –¥–æ–±–∞–≤–ª—è—Ç—å –≤–ª–æ–∂–µ–Ω–∏—è
|
|
|






























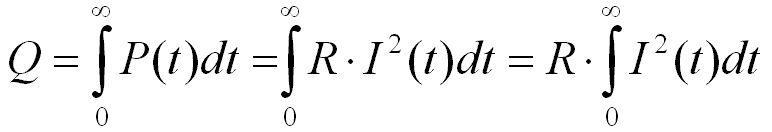 ,
,







