|
–§–æ—Ä—É–º –Ý–∞–¥–∏–æ–ö–æ—Ç • –ü—Ä–æ—Å–º–æ—Ç—Ä —Ç–µ–º—ã - –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.
–°–æ–æ–±—â–µ–Ω–∏—è –±–µ–∑ –æ—Ç–≤–µ—Ç–æ–≤ | –ê–∫—Ç–∏–≤–Ω—ã–µ —Ç–µ–º—ã
 
|
–°—Ç—Ä–∞–Ω–∏—Ü–∞ 170 –∏–∑ 180
|
[ –°–æ–æ–±—â–µ–Ω–∏–π: 3585 ] |
... , , , , , , ... |
| –ê–≤—Ç–æ—Ä |
–°–æ–æ–±—â–µ–Ω–∏–µ |
iddqd84

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü—Ç –¥–µ–∫ 18, 2020 22:47:55 |
|
| –ü–µ—Ä–≤—ã–π —Ä–∞–∑ —Å–∫–∞–∑–∞–ª –ú—è—É! |
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –∏—é–Ω 16, 2014 01:01:37
–°–æ–æ–±—â–µ–Ω–∏–π: 28
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
—Å–∏–º—É–ª—å –≤—Ä—ë—Ç –•–æ—Ç–µ–ª–æ—Å—å –±—ã –∏—Å–ø–æ–ª—å–∑–æ–≤–∞—Ç—å –ü—Ä–æ—Ç–µ—É—Å, —Ç.–∫. —Ö–æ—á—É —Å–º–æ–¥–µ–ª–∏—Ä–æ–≤–∞—Ç—å —Ä–∞–±–æ—Ç—É –ø—Ä–æ—à–∏–≤–∫–∏ AVR 328p. –ß—Ç–æ –¥–µ–ª–∞—Ç—å —Å —Ç–∞–∫–∏–º –ø–æ–≤–µ–¥–µ–Ω–∏–µ–º?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
12943

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –¥–µ–∫ 19, 2020 06:20:36 |
|
–ö–∞—Ä–º–∞: 3
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 728
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –æ–∫—Ç 20, 2016 13:51:03
–°–æ–æ–±—â–µ–Ω–∏–π: 3702
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–ò—Å–ø–æ–ª—å–∑—É–π –¥–ª—è –ú–ö –ø—Ä–æ—Ç–µ–∑, –∞ –¥–ª—è –∞–Ω–∞–ª–æ–≥–æ–≤—ã—Ö —Å—Ö–µ–º –∏–ª–∏ –∞–Ω–∞–ª–æ–≥–æ–≤—ã—Ö —á–∞—Å—Ç–µ–π —Ü–∏—Ñ—Ä–æ–≤—ã—Ö —Å—Ö–µ–º LTspice.
–î–æ–±–∞–≤–ª–µ–Ω–æ after 3 minutes 39 seconds:
–ú–æ–∂–µ—Ç –±—ã—Ç—å –≤ –ø—Ä–æ—Ç–µ–∑–µ —É–¥–∞—Å—Ç—Å—è –Ω–∞–π—Ç–∏ —Ö–æ—Ç—å –æ–¥–Ω—É –ø—Ä–∏–ª–∏—á–Ω—É—é –º–æ–¥–µ–ª—å —Ç—Ä–∞–Ω–∑–∏—Å—Ç–æ—Ä–∞
–∏–ª–∏ —Ä–∞–∑–æ–±—Ä–∞—Ç—å—Å—è –∏ —Å–¥–µ–ª–∞—Ç—å —Å–≤–æ—é –º–æ–¥–µ–ª—å–∫—É.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
iddqd84

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± –¥–µ–∫ 19, 2020 22:53:28 |
|
| –ü–µ—Ä–≤—ã–π —Ä–∞–∑ —Å–∫–∞–∑–∞–ª –ú—è—É! |
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –∏—é–Ω 16, 2014 01:01:37
–°–æ–æ–±—â–µ–Ω–∏–π: 28
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
12943, —Å–ø–∞—Å–∏–±–æ –∑–∞ –æ—Ç–≤–µ—Ç—ã.
–ë–æ–ª–µ–µ-–º–µ–Ω–µ–µ —Ä–∞–±–æ—á–∏—Ö –º–æ–¥–µ–ª–µ–π –º–Ω–æ–≥–æ, –Ω–æ –º–æ–∏ bc807 bc817 –∫ –Ω–∏–º –Ω–µ –æ—Ç–Ω–æ—Å—è—Ç—Å—è. –û—Ä–∏–µ–Ω—Ç–∏—Ä–æ–≤–∞—Ç—å—Å—è –±—É–¥—É –Ω–∞ –í–∞—à–µ –∑–Ω–∞—á–µ–Ω–∏–µ –µ–º–∫–æ—Å—Ç–∏.
–£–≤—ã, LTspice –Ω–µ –ø–æ—Ç—è–Ω—É, –æ—á–µ–Ω—å –æ–≥—Ä–∞–Ω–∏—á–µ–Ω –ø–æ –≤—Ä–µ–º–µ–Ω–∏.
–ë–æ–ª–µ–µ-–º–µ–Ω–µ–µ –æ—Å–≤–æ–∏–ª QUCS –∏ –¥–∞–∂–µ –Ω–∞—É—á–∏–ª—Å—è –æ–±—Ö–æ–¥–∏—Ç—å –≤–µ—á–Ω—É—é –æ—à–∏–±–∫—É "Jacobian singular...".
–ú–æ–∂–Ω–æ –ª–∏ –¥–æ–≤–µ—Ä—è—Ç—å –µ–º—É –¥–ª—è –º–æ–¥–µ–ª–∏—Ä–æ–≤–∞–Ω–∏—è –∞–Ω–∞–ª–æ–≥–æ–≤–æ–π —á–∞—Å—Ç–∏?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
12943

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –¥–µ–∫ 20, 2020 08:14:44 |
|
–ö–∞—Ä–º–∞: 3
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 728
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –æ–∫—Ç 20, 2016 13:51:03
–°–æ–æ–±—â–µ–Ω–∏–π: 3702
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
При такой схеме, С1 является "убийцей" контактов кнопки… если ёмкость нужна, то необходимо добавить ограничивающий резистор для кнопки. Последовательно с конденсатором поставь несколько ом, например 10. Модель транзистора почти не имеет значения, лишь бы не ошибочная. Для такого смешного дела, как моделирование этого ключа, браться за ЛТс может быть и не стоит, проще попросить помощи. Детским игрушкам я бы не доверял, возможно это не спайс, а что-то недопустимо упрощённое.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
spilben

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Ç –¥–µ–∫ 22, 2020 01:34:11 |
|
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –í—Ç –¥–µ–∫ 22, 2020 00:58:40
–°–æ–æ–±—â–µ–Ω–∏–π: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–ó–¥—Ä–∞–≤—Å—Ç–≤—É–π—Ç–µ.
–£ –º–µ–Ω—è –≤–æ–ø—Ä–æ—Å –ø–æ —Ç—Ä–∞–Ω—Å—Ñ–æ—Ä–º–∞—Ç–æ—Ä–∞–º. –ö–∞–∫ —è –ø–æ–Ω—è–ª, –æ–ø—Ä–µ–¥–µ–ª–∏—Ç—å —Ö–∞—Ä–∞–∫—Ç–µ—Ä–∏—Å—Ç–∏–∫–∏ —Ç—Ä–∞–Ω—Å—Ñ–æ—Ä–º–∞—Ç–æ—Ä–∞ –≤–µ—Å—å–º–∞ –Ω–µ –ø—Ä–æ—Å—Ç–æ. –ù–æ –º–æ–∂–µ—Ç –∫–∞–∫-—Ç–æ –º–æ–∂–Ω–æ —Ö–æ—Ç—è –±—ã –≤—ã—è—Å–Ω–∏—Ç—å, –º–æ–∂–Ω–æ –ª–∏ –ø—Ä–æ–∏–∑–≤–æ–ª—å–Ω—ã–π —Ç—Ä–∞–Ω—Å—Ñ–æ—Ä–º–∞—Ç–æ—Ä –ø–æ–¥–∫–ª—é—á–∞—Ç—å –∫ —Å–µ—Ç–∏ 220–≤?
–£ –º–µ–Ω—è –µ—Å—Ç—å –≥–æ—Ä—Å—Ç–∫–∞ –±–µ–∑—ã–º—è–Ω–Ω—ã—Ö —Ç—Ä–∞–Ω—Å—Ñ–æ—Ä–º–∞—Ç–æ—Ä–æ–≤, –Ω—É–∂–Ω–æ –ø–æ–¥–æ–±—Ä–∞—Ç—å —Ç—Ä–∞–Ω—Å—Ñ–æ—Ä–º–∞—Ç–æ—Ä –¥–ª—è –ø—Ä–æ—Å—Ç–æ–≥–æ –≤—ã–ø—Ä—è–º–∏—Ç–µ–ª—è
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
Asaba

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Ç –¥–µ–∫ 22, 2020 10:09:35 |
|
–ö–∞—Ä–º–∞: 62
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 750
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü—Ç –∞–≤–≥ 04, 2017 19:36:00
–°–æ–æ–±—â–µ–Ω–∏–π: 5635
–û—Ç–∫—É–¥–∞: –ø–æ—Å—Ç–Ω—É—Ä—Å—É–ª—Ç–∞–Ω–∞—Ç –ë–æ—Ä–∞—Ç–∏—Å—Ç–∞–Ω
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
lumped.net

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å —è–Ω–≤ 17, 2021 21:32:51 |
|
| –ú—É—á–∏—Ç–µ–ª—å –º–∏–∫—Ä–æ—Å—Ö–µ–º |
–ö–∞—Ä–º–∞: 7
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 198
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°–± —Ñ–µ–≤ 01, 2020 16:04:03
–°–æ–æ–±—â–µ–Ω–∏–π: 425
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–ü–æ–º–æ–≥–∏—Ç–µ –≤—ã—á–∏—Å–ª–∏—Ç—å –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω—ã–π –∏–Ω—Ç–µ–≥—Ä–∞–ª –æ—Ç –ø—Ä–æ–∏–∑–≤–µ–¥–µ–Ω–∏—è –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ –î–∏—Ä–∞–∫–∞ –Ω–∞ —Ñ—É–Ω–∫—Ü–∏—é –µ–¥–∏–Ω–∏—á–Ω–æ–≥–æ —Å–∫–∞—á–∫–∞ –•–µ–≤–∏—Å–∞–π–¥–∞. –ü—Ä–µ–¥–µ–ª—ã –∏–Ω—Ç–µ–≥—Ä–∏—Ä–æ–≤–∞–Ω–∏—è –æ—Ç –º–∏–Ω—É—Å –¥–æ –ø–ª—é—Å –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç–∏. WolframAlpha –Ω–∞ –∑–∞–ø—Ä–æ—Å "integral from -infinity to +infinity theta(t)*delta(t)*dt" —Å–æ–æ–±—â–∞–µ—Ç, —á—Ç–æ —ç—Ç–æ—Ç –∏–Ω—Ç–µ–≥—Ä–∞–ª –Ω–µ —Å—Ö–æ–¥–∏—Ç—Å—è. –ù–æ —è –≤ —ç—Ç–æ –Ω–µ –≤–µ—Ä—é  –ß–µ–º—É –æ–Ω –≤—Å—ë-—Ç–∞–∫–∏ —Ä–∞–≤–µ–Ω? 0? 1? 0.5? 0.25? 0.75? 2.25?
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
mickbell

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å —è–Ω–≤ 17, 2021 23:50:01 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 116
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 4475
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü—Ç –º–∞—Ä 30, 2012 05:17:29
–°–æ–æ–±—â–µ–Ω–∏–π: 15557
–û—Ç–∫—É–¥–∞: –ï–∫–∞—Ç–µ—Ä–∏–Ω–±—É—Ä–≥
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–ß—É—é, —á—Ç–æ —Ç–∞–∫–∏ 0.5, –Ω–æ –∑—É–± –Ω–µ –¥–∞–º.
_________________
–ú–æ—Ä–¥ - –Ω–∏ –ª–∞–ø.
–ú–∞—Ç, –æ–∫–æ –∏ –¥–∞—Ä. –ê –∫–æ–ª–æ–º?
–ú–∞—Å—Å–∞–º –∫–æ—Ç –∏–ª–∏ —Ç–æ—Ä—Ç?
–¢—Ä–æ—Ç–∏–ª –∏ —Ç–æ–∫ –º–∞—Å—Å–∞–º!
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
lumped.net

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 10:23:48 |
|
| –ú—É—á–∏—Ç–µ–ª—å –º–∏–∫—Ä–æ—Å—Ö–µ–º |
–ö–∞—Ä–º–∞: 7
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 198
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°–± —Ñ–µ–≤ 01, 2020 16:04:03
–°–æ–æ–±—â–µ–Ω–∏–π: 425
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
|
–Ý–µ–∫–ª–∞–º–∞
|
|
|
|
|
|
|
|
 |
El-Eng

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 10:55:09 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 97
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1581
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 26, 2012 14:44:34
–°–æ–æ–±—â–µ–Ω–∏–π: 3724
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 1
–ú–µ–¥–∞–ª–∏: 1

|
lumped.net –ø–∏—Å–∞–ª(–∞): –ü–æ–º–æ–≥–∏—Ç–µ –≤—ã—á–∏—Å–ª–∏—Ç—å –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω—ã–π –∏–Ω—Ç–µ–≥—Ä–∞–ª –æ—Ç –ø—Ä–æ–∏–∑–≤–µ–¥–µ–Ω–∏—è –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ –î–∏—Ä–∞–∫–∞ –Ω–∞ —Ñ—É–Ω–∫—Ü–∏—é –µ–¥–∏–Ω–∏—á–Ω–æ–≥–æ —Å–∫–∞—á–∫–∞ –•–µ–≤–∏—Å–∞–π–¥–∞. –ï—Å–ª–∏ –í—ã –Ω–µ –∑–Ω–∞–∫–æ–º—ã —Å –∫–Ω–∏–≥–æ–π –£.–ú. –°–∏–±–µ—Ä—Ç, "–¶–µ–ø–∏, —Å–∏–≥–Ω–∞–ª—ã, —Å–∏—Å—Ç–µ–º—ã", –≤ 2 —á–∞—Å—Ç—è—Ö, –ú., –ú–∏—Ä, 1988, —Ç–æ —Å–æ–≤–µ—Ç—É—é –ø–æ–∑–Ω–∞–∫–æ–º–∏—Ç—å—Å—è (–µ—ë –º–æ–∂–Ω–æ –Ω–∞–π—Ç–∏ –≤ –ò–Ω—Ç–µ—Ä–Ω–µ—Ç–µ). –¢–∞–º –í—ã –Ω–∞–π–¥–µ—Ç–µ –º–Ω–æ–≥–æ –∏–Ω—Ç–µ—Ä–µ—Å–Ω–æ–≥–æ, –≤ —á–∞—Å—Ç–Ω–æ—Å—Ç–∏, –≤ –ì–ª–∞–≤–µ 11 —Ä–∞—Å—Å–º–∞—Ç—Ä–∏–≤–∞–µ—Ç—Å—è –∏ —ç—Ç–æ—Ç –≤–æ–ø—Ä–æ—Å.
_________________
Like the eyes of a cat in the black and blue...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
mickbell

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 18:41:18 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 116
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 4475
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü—Ç –º–∞—Ä 30, 2012 05:17:29
–°–æ–æ–±—â–µ–Ω–∏–π: 15557
–û—Ç–∫—É–¥–∞: –ï–∫–∞—Ç–µ—Ä–∏–Ω–±—É—Ä–≥
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
|
–ê —á—Ç–æ —Ç–∞–º, —á—Ç–æ–±—ã –Ω–µ —á–∏—Ç–∞—Ç—å? –ú–Ω–µ –≤–æ—Ç —Å–æ–≤—Å–µ–º –Ω–µ–∫–æ–≥–¥–∞...
–ß—Ç–æ –∫–∞—Å–∞–µ—Ç—Å—è –∑–∞–¥–∞–Ω–Ω–æ–≥–æ –≤–æ–ø—Ä–æ—Å–∞, —Ç–æ —è —Ä–∞—Å—Å—É–∂–¥–∞–ª –ø—Ä–æ—Å—Ç—ã–º, –∫–∞–∫ –≤–∞–ª–µ–Ω–æ–∫, –æ–±—Ä–∞–∑–æ–º. –í–æ–∑–º–æ–∂–Ω–æ, –Ω–µ–ø—Ä–∞–≤–∏–ª—å–Ω–æ. –ü—Ä–µ–¥—Å—Ç–∞–≤–∏–º —Å–µ–±–µ –Ω–µ–∫–∏–π –∏–º–ø—É–ª—å—Å, —Å–∏–º–º–µ—Ç—Ä–∏—á–Ω—ã–π –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ –æ—Å–∏ –æ—Ä–¥–∏–Ω–∞—Ç (u). –û—Å—å –∞–±—Å—Ü–∏—Å—Å - –≤—Ä–µ–º—è (t). –ü–ª–æ—â–∞–¥—å —ç—Ç–æ–≥–æ –∏–º–ø—É–ª—å—Å–∞ —Ç–æ–∂–µ –µ–¥–∏–Ω–∏—á–Ω–∞—è, –∫–∞–∫ –∏ —É –¥–µ–ª—å—Ç–∞-–∏–º–ø—É–ª—å—Å–∞, —Ñ–æ—Ä–º–∞ –Ω–µ –∏–º–µ–µ—Ç –∑–Ω–∞—á–µ–Ω–∏—è. –î—Ä—É–≥–æ–π –∏–º–ø—É–ª—å—Å - –µ–¥–∏–Ω–∏—á–Ω–∞—è —Å—Ç—É–ø–µ–Ω—å–∫–∞: —Å–ª–µ–≤–∞ –æ—Ç –æ—Å–∏ –æ—Ä–¥–∏–Ω–∞—Ç –æ–Ω–∞ –Ω—É–ª–µ–≤–∞—è, —Å–ø—Ä–∞–≤–∞ - –µ–¥–∏–Ω–∏—á–Ω–∞—è. –ï—Å–ª–∏ –æ–¥–Ω–æ –ø–µ—Ä–µ–º–Ω–æ–∂–∏–º –Ω–∞ –¥—Ä—É–≥–æ–µ, —Ç–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª –ø–æ–ª—É—á–∞–µ—Ç—Å—è, –ø–æ–Ω—è—Ç–Ω–æ, 0.5. –ê —Ç–µ–ø–µ—Ä—å —Å–∂–∏–º–∞–µ–º —ç—Ç–æ—Ç –∏–º–ø—É–ª—å—Å –ø–æ –≥–æ—Ä–∏–∑–æ–Ω—Ç–∞–ª–∏, —Å—Ç—Ä–µ–º—è—Å—å –∫ –Ω—É–ª–µ–≤–æ–π –µ–≥–æ —à–∏—Ä–∏–Ω–µ; –∞–º–ø–ª–∏—Ç—É–¥–∞ –µ–≥–æ, –µ—Å—Ç–µ—Å—Ç–≤–µ–Ω–Ω–æ, —É–≤–µ–ª–∏—á–∏–≤–∞–µ—Ç—Å—è. –ù–æ –≤—Å—è–∫–∏–π —Ä–∞–∑ –ø–µ—Ä–µ—Ö–æ–¥ —Å—Ç—É–ø–µ–Ω—å–∫–∏ –∏–∑ –Ω—É–ª—è –≤ –µ–¥–∏–Ω–∏—Ü—É —Ä–µ–∂–µ—Ç —ç—Ç–æ –Ω–∞—à–µ –ø–æ–¥–æ–±–∏–µ –¥–µ–ª—å—Ç–∞-–∏–º–ø—É–ª—å—Å–∞ —Ä–æ–≤–Ω–æ –ø–æ–ø–æ–ª–∞–º, –∏ —è –Ω–µ –≤–∏–∂—É –ø—Ä–∏—á–∏–Ω—ã, –ø–æ—á–µ–º—É —Ç–∞–∫–æ–µ –ø–æ–ª–æ–∂–µ–Ω–∏–µ –≤–µ—â–µ–π –Ω–µ —Å–æ—Ö—Ä–∞–Ω–∏—Ç—Å—è –≤ –ø—Ä–µ–¥–µ–ª–µ.
_________________
–ú–æ—Ä–¥ - –Ω–∏ –ª–∞–ø.
–ú–∞—Ç, –æ–∫–æ –∏ –¥–∞—Ä. –ê –∫–æ–ª–æ–º?
–ú–∞—Å—Å–∞–º –∫–æ—Ç –∏–ª–∏ —Ç–æ—Ä—Ç?
–¢—Ä–æ—Ç–∏–ª –∏ —Ç–æ–∫ –º–∞—Å—Å–∞–º!
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
lumped.net

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 19:29:58 |
|
| –ú—É—á–∏—Ç–µ–ª—å –º–∏–∫—Ä–æ—Å—Ö–µ–º |
–ö–∞—Ä–º–∞: 7
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 198
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°–± —Ñ–µ–≤ 01, 2020 16:04:03
–°–æ–æ–±—â–µ–Ω–∏–π: 425
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
mickbell, –ø–æ—Å–º–æ—Ç—Ä–∏—Ç–µ –º–æ–∏ —Å—Å—ã–ª–∫–∏, —Ç–∞–º —Å–æ–≤—Å–µ–º –∫—Ä–∞—Ç–∫–æ –æ–ø–∏—Å–∞–Ω–æ. –ï–¥–∏–Ω–∏—á–Ω—ã–π —Å–∫–∞—á–æ–∫ –∏–º–µ–µ—Ç –Ω–µ—É—Å—Ç—Ä–∞–Ω–∏–º—ã–π —Ä–∞–∑—Ä—ã–≤ –ø–µ—Ä–≤–æ–≥–æ —Ä–æ–¥–∞, –ø–æ—ç—Ç–æ–º—É –≤—Å—è —ç—Ç–∞ –ª–æ–≥–∏–∫–∞ –Ω–µ —Ä–∞–±–æ—Ç–∞–µ—Ç, —É–≤—ã. –°–∞–º —Ä–∞—Å—Å—É–∂–¥–∞–ª —Ç–∞–∫ –∂–µ. El-Eng, –æ—Ç–ª–∏—á–Ω–æ, —Å–ø–∞—Å–∏–±–æ, —ç—Ç–æ —Ç–æ, —á—Ç–æ –Ω—É–∂–Ω–æ! –í–æ—Ç —Ç–∞–º –∞–≤—Ç–æ—Ä —Ä–∞—Å—Å–º–∞—Ç—Ä–∏–≤–∞–µ—Ç –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–Ω—ã–π –ø–∞—Ä–∞–¥–æ–∫—Å –∏ –ø–∏—à–µ—Ç, —á—Ç–æ –Ω–µ–≤–æ–∑–º–æ–∂–Ω–æ –Ω–∞–π—Ç–∏ —ç–Ω–µ—Ä–≥–∏—é, –∫–æ—Ç–æ—Ä–∞—è –±—ã–ª–∞ –ø–æ—Ç—Ä–∞—á–µ–Ω–∞ –±–∞—Ç–∞—Ä–µ–µ–π, –∏–∑-–∑–∞ —Ç–æ–≥–æ, —á—Ç–æ –Ω–µ —Å—Ö–æ–¥–∏—Ç—Å—è –æ–±—Å—É–∂–¥–∞–µ–º—ã–π –∏–Ω—Ç–µ–≥—Ä–∞–ª. –ê —á—Ç–æ –µ—Å–ª–∏ –¥–æ–±–∞–≤–∏—Ç—å –≤ —Å—Ö–µ–º—É –º–æ–¥–µ–ª—å –∫–ª—é—á–∞? 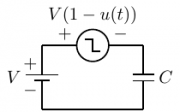 –ï–¥–∏–Ω–∏—á–Ω—ã–π —Å–∫–∞—á–æ–∫ –•–µ–≤–∏—Å–∞–π–¥–∞ —è –æ–±–æ–∑–Ω–∞—á–∏–ª u(t), –∫–∞–∫ —É –∞–≤—Ç–æ—Ä–∞. –í—Ä–µ–º—è —Ä–∞—Å—Å–º–∞—Ç—Ä–∏–≤–∞–µ—Ç—Å—è –æ—Ç -–±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç–∏ –¥–æ +–±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç–∏. –¢–µ–ø–µ—Ä—å –∏–Ω—Ç–µ–≥—Ä–∞–ª –º–æ—â–Ω–æ—Å—Ç–∏ –Ω–∞ –±–∞—Ç–∞—Ä–µ–µ –≤—ã—á–∏—Å–ª—è–µ—Ç—Å—è –±–µ–∑ –ø—Ä–æ–±–ª–µ–º. –ü–æ–ª—É—á–∞–µ—Ç—Å—è, —á—Ç–æ –±–∞—Ç–∞—Ä–µ—è –ø–æ—Ç—Ä–∞—Ç–∏–ª–∞ V*V*C [–î–∂]. –ù–∞ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–µ –∏ –∫–ª—é—á–µ –∏–∑-–∑–∞ –Ω–µ—Å—Ö–æ–¥—è—â–µ–≥–æ—Å—è –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞ —ç–Ω–µ—Ä–≥–∏—è –≤–ø—Ä—è–º—É—é –Ω–µ –≤—ã—á–∏—Å–ª—è–µ—Ç—Å—è, –Ω–æ –ø–æ –∏—Ç–æ–≥—É –∏–∑–≤–µ—Å—Ç–Ω–æ, —á—Ç–æ –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä –∑–∞–ø–∞—Å V*V*C/2 [–î–∂]. –ö—É–¥–∞ —É—à–ª–∞ –¥—Ä—É–≥–∞—è –ø–æ–ª–æ–≤–∏–Ω–∞ —ç–Ω–µ—Ä–≥–∏–∏? - –≤—ã—Ö–æ–¥–∏—Ç —á—Ç–æ –≤ –∫–ª—é—á, –ø–æ—Å–∫–æ–ª—å–∫—É –Ω–∏–∫–∞–∫–∏—Ö –¥—Ä—É–≥–∏—Ö —ç–ª–µ–º–µ–Ω—Ç–æ–≤ –≤ —Å—Ö–µ–º–µ –Ω–µ—Ç. –ü–∞—Ä–∞–¥–æ–∫—Å –ø—Ä–µ–æ–¥–æ–ª—ë–Ω (—à—É—Ç–∫–∞).
–ü–æ—Å–ª–µ–¥–Ω–∏–π —Ä–∞–∑ —Ä–µ–¥–∞–∫—Ç–∏—Ä–æ–≤–∞–ª–æ—Å—å lumped.net –ü–Ω —è–Ω–≤ 18, 2021 19:49:05, –≤—Å–µ–≥–æ —Ä–µ–¥–∞–∫—Ç–∏—Ä–æ–≤–∞–ª–æ—Å—å 1 —Ä–∞–∑.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
El-Eng

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 19:46:22 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 97
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1581
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 26, 2012 14:44:34
–°–æ–æ–±—â–µ–Ω–∏–π: 3724
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 1
–ú–µ–¥–∞–ª–∏: 1

|
mickbell –ø–∏—Å–∞–ª(–∞): –ê —á—Ç–æ —Ç–∞–º, —á—Ç–æ–±—ã –Ω–µ —á–∏—Ç–∞—Ç—å? –ú–Ω–µ –≤–æ—Ç —Å–æ–≤—Å–µ–º –Ω–µ–∫–æ–≥–¥–∞... –≠-—ç-—ç, —ç—Ç–∞ –∫–Ω–∏–≥–∞ –Ω–∞–ø–∏—Å–∞–Ω–∞ –º–∞—Ç–µ–º–∞—Ç–∏–∫–æ–º, –∏ —á—Ç–æ–±—ã –ø—Ä–æ–Ω–∏–∫–Ω—É—Ç—å—Å—è –≤—Å–µ–π –µ—ë –≥–ª—É–±–∏–Ω–æ–π, –µ—ë –Ω–∞–¥–æ —á–∏—Ç–∞—Ç—å (–µ—Å–ª–∏ —Ö–≤–∞—Ç–∏—Ç —Å–∏–ª  ). –ù–æ –ø–æ–ø—Ä–æ–±—É—é –∫–æ—Ä–æ—Ç–∫–æ —Å—Ñ–æ—Ä–º—É–ª–∏—Ä–æ–≤–∞—Ç—å —Å–∫–∞–∑–∞–Ω–Ω–æ–µ –Ω–∞ —Å—Ç—Ä. 15-16 —á–∞—Å—Ç–∏ 2. –î–µ–ª–æ –≤ —Ç–æ–º, –ø—Ä–æ–∏–∑–≤–µ–¥–µ–Ω–∏–µ –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ –î–∏—Ä–∞–∫–∞ –Ω–∞ –∫–∞–∫—É—é-–ª–∏–±–æ –≥–ª–∞–¥–∫—É—é —Ñ—É–Ω–∫—Ü–∏—é –∑–∞–≤–∏—Å–∏—Ç —Ç–æ–ª—å–∫–æ –æ—Ç –∑–Ω–∞—á–µ–Ω–∏—è —ç—Ç–æ–π —Ñ—É–Ω–∫—Ü–∏–∏ –≤ –Ω—É–ª–µ–≤–æ–π —Ç–æ—á–∫–µ. –ù–æ –≤–∞–∂–Ω–æ, —á—Ç–æ–±—ã —Ñ—É–Ω–∫—Ü–∏—è –±—ã–ª–∞ –≥–ª–∞–¥–∫–æ–π, —Ç.–µ. –µ—ë —Å—Ä–µ–¥–Ω–µ–µ –∑–Ω–∞—á–µ–Ω–∏–µ –≤ –æ–∫—Ä–µ—Å—Ç–Ω–æ—Å—Ç–∏ –Ω—É–ª—è –∏ –∑–Ω–∞—á–µ–Ω–∏–µ –≤ –Ω—É–ª–µ –±—ã–ª–∏ —Ä–∞–≤–Ω—ã. –§—É–Ω–∫—Ü–∏—è –•–µ–≤–∏—Å–∞–π–¥–∞ —Ä–∞–∑—Ä—ã–≤–Ω–∞ –≤ –Ω—É–ª–µ, –∏ –ø–æ—ç—Ç–æ–º—É –¥–ª—è –ø—Ä–æ–∏–∑–≤–µ–¥–µ–Ω–∏—è –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ –î–∏—Ä–∞–∫–∞ –∏ —Ñ—É–Ω–∫—Ü–∏–∏ –•–µ–≤–∏—Å–∞–π–¥–∞ "... –Ω–µ–≤–æ–∑–º–æ–∂–Ω–æ –Ω–∞–π—Ç–∏ —Å–æ–≤–º–µ—Å—Ç–∏–º–æ–µ —Å —ç—Ç–æ–π —Å–∏—Ç—É–∞—Ü–∏–µ–π –∑–Ω–∞—á–µ–Ω–∏–µ, –∏ –ø–æ —ç—Ç–æ–π –ø—Ä–∏—á–∏–Ω–µ –µ–µ —Å–ª–µ–¥—É–µ—Ç –∏–∑–±–µ–≥–∞—Ç—å", —Ç.–µ. –∏–Ω—Ç–µ–≥—Ä–∞–ª —ç—Ç–æ–≥–æ –ø—Ä–æ–∏–∑–≤–µ–¥–µ–Ω–∏—è –Ω–µ –∏–º–µ–µ—Ç –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω–æ–≥–æ –∑–Ω–∞—á–µ–Ω–∏—è. lumped.net –ø–∏—Å–∞–ª(–∞): El-Eng, –æ—Ç–ª–∏—á–Ω–æ, —Å–ø–∞—Å–∏–±–æ, —ç—Ç–æ —Ç–æ, —á—Ç–æ –Ω—É–∂–Ω–æ! –ü–æ–∂–∞–ª—É–π—Å—Ç–∞!
_________________
Like the eyes of a cat in the black and blue...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
mickbell

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 20:04:52 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 116
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 4475
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü—Ç –º–∞—Ä 30, 2012 05:17:29
–°–æ–æ–±—â–µ–Ω–∏–π: 15557
–û—Ç–∫—É–¥–∞: –ï–∫–∞—Ç–µ—Ä–∏–Ω–±—É—Ä–≥
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–°–ø–∞—Å–∏–±–æ –≤–∞–º –æ–±–æ–∏–º, –∫–∞–∂–µ—Ç—Å—è, —è –ø–æ–Ω—è–ª. –î–æ–±–∞–≤–ª–µ–Ω–æ after 5 minutes 28 seconds:–ö—É–¥–∞ —É—à–ª–∞ –¥—Ä—É–≥–∞—è –ø–æ–ª–æ–≤–∏–Ω–∞ —ç–Ω–µ—Ä–≥–∏–∏? - –≤—ã—Ö–æ–¥–∏—Ç —á—Ç–æ –≤ –∫–ª—é—á, –ø–æ—Å–∫–æ–ª—å–∫—É –Ω–∏–∫–∞–∫–∏—Ö –¥—Ä—É–≥–∏—Ö —ç–ª–µ–º–µ–Ω—Ç–æ–≤ –≤ —Å—Ö–µ–º–µ –Ω–µ—Ç. –ü–∞—Ä–∞–¥–æ–∫—Å –ø—Ä–µ–æ–¥–æ–ª—ë–Ω (—à—É—Ç–∫–∞). –í –∫–∞–∂–¥–æ–π —à—É—Ç–∫–µ –µ—Å—Ç—å –¥–æ–ª—è —à—É—Ç–∫–∏. –ò–º–µ–Ω–Ω–æ –≤ –∫–ª—é—á. –ß—Ç–æ–±—ã —ç—Ç–æ —Ä–µ—à–∏–ª–æ—Å—å, —Ü–µ–ø—å –æ–±—è–∑–∞–Ω–∞ –±—ã—Ç—å —Å –ø–æ—Ç–µ—Ä—è–º–∏ - –∏–ª–∏ –æ–º–∏—á–µ—Å–∫–∏–º–∏ (–≤ —Ç–æ–º –∂–µ –∫–ª—é—á–µ), –∏–ª–∏ –Ω–∞–¥–æ –¥–æ–ø—É—Å—Ç–∏—Ç—å –Ω–∞–ª–∏—á–∏–µ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç–∏ –∏ —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω–æ–≥–æ –ø–æ–ª—è. PS. –ù—É –Ω–∏—Ñ–∏–≥–∞ —Å–µ–±–µ "—ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã"...
_________________
–ú–æ—Ä–¥ - –Ω–∏ –ª–∞–ø.
–ú–∞—Ç, –æ–∫–æ –∏ –¥–∞—Ä. –ê –∫–æ–ª–æ–º?
–ú–∞—Å—Å–∞–º –∫–æ—Ç –∏–ª–∏ —Ç–æ—Ä—Ç?
–¢—Ä–æ—Ç–∏–ª –∏ —Ç–æ–∫ –º–∞—Å—Å–∞–º!
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
lumped.net

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 20:21:04 |
|
| –ú—É—á–∏—Ç–µ–ª—å –º–∏–∫—Ä–æ—Å—Ö–µ–º |
–ö–∞—Ä–º–∞: 7
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 198
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°–± —Ñ–µ–≤ 01, 2020 16:04:03
–°–æ–æ–±—â–µ–Ω–∏–π: 425
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–ù–æ –≤–∞–∂–Ω–æ, —á—Ç–æ–±—ã —Ñ—É–Ω–∫—Ü–∏—è –±—ã–ª–∞ –≥–ª–∞–¥–∫–æ–π, —Ç.–µ. –µ—ë —Å—Ä–µ–¥–Ω–µ–µ –∑–Ω–∞—á–µ–Ω–∏–µ –≤ –æ–∫—Ä–µ—Å—Ç–Ω–æ—Å—Ç–∏ –Ω—É–ª—è –∏ –∑–Ω–∞—á–µ–Ω–∏–µ –≤ –Ω—É–ª–µ –±—ã–ª–∏ —Ä–∞–≤–Ω—ã. –ï—Å–ª–∏ —Å–ª–µ–¥–æ–≤–∞—Ç—å —ç—Ç–æ–π —Ñ–æ—Ä–º—É–ª–∏—Ä–æ–≤–∫–µ, —Ç–æ –º–æ–∂–Ω–æ –≤—ã—á–∏—Å–ª–∏—Ç—å –∏–Ω—Ç–µ–≥—Ä–∞–ª –ø—Ä–æ–∏–∑–≤–µ–¥–µ–Ω–∏—è –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ –Ω–∞ —Ñ—É–Ω–∫—Ü–∏—é sgn(x), –ø–æ—Å–∫–æ–ª—å–∫—É —Å—Ä–µ–¥–Ω–µ–µ –ø—Ä–µ–¥–µ–ª–æ–≤ —Å–ø—Ä–∞–≤–∞ –∏ —Å–ª–µ–≤–∞ –æ—Ç –Ω—É–ª—è —Ä–∞–≤–Ω–æ –∑–Ω–∞—á–µ–Ω–∏—é —Ñ—É–Ω–∫—Ü–∏–∏ –≤ –Ω—É–ª–µ. –î–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ, WolframAlpha –≤—ã—á–∏—Å–ª—è–µ—Ç —ç—Ç–æ—Ç –∏–Ω—Ç–µ–≥—Ä–∞–ª –∫–∞–∫ integral from -infinity to +infinity delta(t)*sgn(t)*dt = 0. –¢–æ–≥–¥–∞ –º–æ–∂–Ω–æ –≤—ã—á–∏—Å–ª–∏—Ç—å –∏ –∏–Ω—Ç–µ–≥—Ä–∞–ª –æ—Ç –ø—Ä–æ–∏–∑–≤–µ–¥–µ–Ω–∏—è –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ –Ω–∞ –µ–¥–∏–Ω–∏—á–Ω—ã–π —Å–∫–∞—á–æ–∫, –Ω–æ –Ω—É–∂–Ω–æ —á—Ç–æ–±—ã –æ–Ω –∏–º–µ–ª –∑–Ω–∞—á–µ–Ω–∏–µ 1/2 –≤ –º–æ–º–µ–Ω—Ç –ø–µ—Ä–µ–∫–ª—é—á–µ–Ω–∏—è. –ò–Ω–∞—á–µ –æ–Ω –Ω–µ –≤—ã—Ä–∞–∂–∞–µ—Ç—Å—è —á–µ—Ä–µ–∑ sgn(x). –í –æ–±—â–µ–º, –≤—ã—à–µ —è –Ω–µ–ø—Ä–∞–≤–∏–ª—å–Ω—ã–π –∞—Ä–≥—É–º–µ–Ω—Ç –ø—Ä–∏–≤–µ–ª: —Ñ—É–Ω–∫—Ü–∏—è –º–æ–∂–µ—Ç –±—ã—Ç—å —Ä–∞–∑—Ä—ã–≤–Ω–æ–π. mickbell –ø–∏—Å–∞–ª(–∞): –ò–º–µ–Ω–Ω–æ –≤ –∫–ª—é—á. –ß—Ç–æ–±—ã —ç—Ç–æ —Ä–µ—à–∏–ª–æ—Å—å, —Ü–µ–ø—å –æ–±—è–∑–∞–Ω–∞ –±—ã—Ç—å —Å –ø–æ—Ç–µ—Ä—è–º–∏ - –∏–ª–∏ –æ–º–∏—á–µ—Å–∫–∏–º–∏ (–≤ —Ç–æ–º –∂–µ –∫–ª—é—á–µ), –∏–ª–∏ –Ω–∞–¥–æ –¥–æ–ø—É—Å—Ç–∏—Ç—å –Ω–∞–ª–∏—á–∏–µ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç–∏ –∏ —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω–æ–≥–æ –ø–æ–ª—è. –ê —ç—Ç–æ —É–∂–µ –¥–µ—Ç–∞–ª–∏ —Ä–µ–∞–ª–∏–∑–∞—Ü–∏–∏ –∫–ª—é—á–∞. –î–∞–≤–Ω–æ —Ö–æ—Ç–µ–ª –∏–∑–∂–∏—Ç—å —ç—Ç–æ—Ç –ø–∞—Ä–∞–¥–æ–∫—Å, –Ω–æ –≤—Å—ë –∫–∞–∫-—Ç–æ –Ω–µ –ø–æ–ª—É—á–∞–ª–æ—Å—å 
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
El-Eng

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 20:59:38 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 97
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1581
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 26, 2012 14:44:34
–°–æ–æ–±—â–µ–Ω–∏–π: 3724
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ú–µ–¥–∞–ª–∏: 1

|
lumped.net –ø–∏—Å–∞–ª(–∞): –¢–æ–≥–¥–∞ –º–æ–∂–Ω–æ –≤—ã—á–∏—Å–ª–∏—Ç—å –∏ –∏–Ω—Ç–µ–≥—Ä–∞–ª –æ—Ç –ø—Ä–æ–∏–∑–≤–µ–¥–µ–Ω–∏—è –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ –Ω–∞ –µ–¥–∏–Ω–∏—á–Ω—ã–π —Å–∫–∞—á–æ–∫, –Ω–æ –Ω—É–∂–Ω–æ —á—Ç–æ–±—ã –æ–Ω –∏–º–µ–ª –∑–Ω–∞—á–µ–Ω–∏–µ 1/2 –≤ –º–æ–º–µ–Ω—Ç –ø–µ—Ä–µ–∫–ª—é—á–µ–Ω–∏—è. –ß—Ç–æ-—Ç–æ –º–Ω–µ –ø–æ–¥—Å–∫–∞–∑—ã–≤–∞–µ—Ç, —á—Ç–æ —Ç–∞–∫–æ–π –µ–¥–∏–Ω–∏—á–Ω—ã–π —Å–∫–∞—á–æ–∫ —É–∂–µ –Ω–µ –±—É–¥–µ—Ç —Ñ—É–Ω–∫—Ü–∏–µ–π –•–µ–≤–∏—Å–∞–π–¥–∞. mickbell –ø–∏—Å–∞–ª(–∞): –ù—É –Ω–∏—Ñ–∏–≥–∞ —Å–µ–±–µ "—ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã"... 
_________________
Like the eyes of a cat in the black and blue...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
lumped.net

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 22:17:53 |
|
| –ú—É—á–∏—Ç–µ–ª—å –º–∏–∫—Ä–æ—Å—Ö–µ–º |
–ö–∞—Ä–º–∞: 7
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 198
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°–± —Ñ–µ–≤ 01, 2020 16:04:03
–°–æ–æ–±—â–µ–Ω–∏–π: 425
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
–ß—Ç–æ-—Ç–æ –º–Ω–µ –ø–æ–¥—Å–∫–∞–∑—ã–≤–∞–µ—Ç, —á—Ç–æ —Ç–∞–∫–æ–π –µ–¥–∏–Ω–∏—á–Ω—ã–π —Å–∫–∞—á–æ–∫ —É–∂–µ –Ω–µ –±—É–¥–µ—Ç —Ñ—É–Ω–∫—Ü–∏–µ–π –•–µ–≤–∏—Å–∞–π–¥–∞. –ï—Å—Ç—å –∫–∞–∫ –º–∏–Ω–∏–º—É–º 4 –≤–∞—Ä–∏–∞–Ω—Ç–∞: u(0)=0, u(0)=1, u(0)=1/2, u(0)=[0,1]. mickbell –ø–∏—Å–∞–ª(–∞): –ù—É –Ω–∏—Ñ–∏–≥–∞ —Å–µ–±–µ "—ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã"... –í –æ–±—â–µ–º, –µ—Å–ª–∏ —è –Ω–µ –ø—Ä–∞–≤–∏–ª—å–Ω–æ –ø–æ–Ω—è–ª, —Ç–æ –ø–æ–ø—Ä–∞–≤—å—Ç–µ –º–µ–Ω—è. –ï—Å—Ç—å —Ç—Ä–∏ —Å–ª—É—á–∞—è –≤—ã—á–∏—Å–ª–µ–Ω–∏—è –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω–æ–≥–æ –∏–Ω—Ç–µ–≥—Ä–∞–ª–∞ –æ—Ç –¥–µ–ª—å—Ç–∞(t)*f(t)*dt: - –§—É–Ω–∫—Ü–∏—è f(t) –Ω–µ–ø—Ä–µ—Ä—ã–≤–Ω–∞ –≤ —Ç–æ—á–∫–µ t=0. –¢–æ–≥–¥–∞ –ø–æ —Ñ–∏–ª—å—Ç—Ä—É—é—â–µ–º—É —Å–≤–æ–π—Å—Ç–≤—É –¥–µ–ª—å—Ç–∞-—Ñ—É–Ω–∫—Ü–∏–∏ –∏–Ω—Ç–µ–≥—Ä–∞–ª —Ä–∞–≤–µ–Ω f(0).
- –§—É–Ω–∫—Ü–∏—è f(t) –∏–º–µ–µ—Ç —É—Å—Ç—Ä–∞–Ω–∏–º—ã–π —Ä–∞–∑—Ä—ã–≤ –ø–µ—Ä–≤–æ–≥–æ —Ä–æ–¥–∞ –≤ —Ç–æ—á–∫–µ t=0. –¢–æ–≥–¥–∞ –∏–Ω—Ç–µ–≥—Ä–∞–ª —Ä–∞–≤–µ–Ω –ø—Ä–µ–¥–µ–ª—É —Ñ—É–Ω–∫—Ü–∏–∏ –ø—Ä–∏ t->0.
- –§—É–Ω–∫—Ü–∏—è f(t) –∏–º–µ–µ—Ç –Ω–µ—É—Å—Ç—Ä–∞–Ω–∏–º—ã–π —Ä–∞–∑—Ä—ã–≤ –ø–µ—Ä–≤–æ–≥–æ —Ä–æ–¥–∞ –≤ —Ç–æ—á–∫–µ t=0. –¢–æ–≥–¥–∞ –∏–Ω—Ç–µ–≥—Ä–∞–ª —Ä–∞–≤–µ–Ω f(0), –Ω–æ —Ç–æ–ª—å–∫–æ –µ—Å–ª–∏ —Å—Ä–µ–¥–Ω–µ–µ –∑–Ω–∞—á–µ–Ω–∏–µ –º–µ–∂–¥—É –ø—Ä–µ–¥–µ–ª–æ–º —Å–ª–µ–≤–∞ –∏ —Å–ø—Ä–∞–≤–∞ –æ—Ç 0 —Ç–æ–∂–µ —Ä–∞–≤–Ω–æ f(0).
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
El-Eng

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –ü–Ω —è–Ω–≤ 18, 2021 22:40:21 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 97
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1581
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 26, 2012 14:44:34
–°–æ–æ–±—â–µ–Ω–∏–π: 3724
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ú–µ–¥–∞–ª–∏: 1

|
lumped.net –ø–∏—Å–∞–ª(–∞): –ï—Å—Ç—å –∫–∞–∫ –º–∏–Ω–∏–º—É–º 4 –≤–∞—Ä–∏–∞–Ω—Ç–∞... –ê–≥–∞, –≤–∏–¥–∏–º–æ –ø–æ—ç—Ç–æ–º—É –°–∏–±–µ—Ä—Ç –∏ —Å–æ–≤–µ—Ç—É–µ—Ç –∏–∑–±–µ–≥–∞—Ç—å —Ç–∞–∫–æ–π —Å–∏—Ç—É–∞—Ü–∏–∏. –•–º, —Ö–æ—Ä–æ—à–∞—è —Ç–µ–º–∞ –¥–ª—è –≤—Å—Ç—Ä–µ—á–∏ –º–∞—Ç–µ–º–∞—Ç–∏–∫–æ–≤ –∑–∞ –±—É—Ç—ã–ª–∫–æ–π –ö–ª–µ–π–Ω–∞.  lumped.net –ø–∏—Å–∞–ª(–∞): ... –µ—Å–ª–∏ —è –Ω–µ –ø—Ä–∞–≤–∏–ª—å–Ω–æ –ø–æ–Ω—è–ª ... –î—É–º–∞—é, –≤—Å–µ –ø—Ä–∞–≤–∏–ª—å–Ω–æ.
_________________
Like the eyes of a cat in the black and blue...
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
lumped.net

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± —è–Ω–≤ 23, 2021 00:50:14 |
|
| –ú—É—á–∏—Ç–µ–ª—å –º–∏–∫—Ä–æ—Å—Ö–µ–º |
–ö–∞—Ä–º–∞: 7
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 198
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°–± —Ñ–µ–≤ 01, 2020 16:04:03
–°–æ–æ–±—â–µ–Ω–∏–π: 425
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
mickbell –ø–∏—Å–∞–ª(–∞): –ò–º–µ–Ω–Ω–æ –≤ –∫–ª—é—á. –ß—Ç–æ–±—ã —ç—Ç–æ —Ä–µ—à–∏–ª–æ—Å—å, —Ü–µ–ø—å –æ–±—è–∑–∞–Ω–∞ –±—ã—Ç—å —Å –ø–æ—Ç–µ—Ä—è–º–∏ - –∏–ª–∏ –æ–º–∏—á–µ—Å–∫–∏–º–∏ (–≤ —Ç–æ–º –∂–µ –∫–ª—é—á–µ), –∏–ª–∏ –Ω–∞–¥–æ –¥–æ–ø—É—Å—Ç–∏—Ç—å –Ω–∞–ª–∏—á–∏–µ –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç–∏ –∏ —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω–æ–≥–æ –ø–æ–ª—è. –í—Å—ë –æ–∫–∞–∑–∞–ª–æ—Å—å –µ—â—ë –∏–Ω—Ç–µ—Ä–µ—Å–Ω–µ–µ. –í–æ—Ç —Å—Ç–∞—Ç—å—è, –≤ –∫–æ—Ç–æ—Ä–æ–π –∞–≤—Ç–æ—Ä —Ä–∞—Å—Å–º–∞—Ç—Ä–∏–≤–∞–µ—Ç —Ç–∞–∫—É—é –∂–µ —Å—Ö–µ–º—É (–±–∞—Ç–∞—Ä–µ—è, –∫–ª—é—á, –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä) –∏ —É—Ç–≤–µ—Ä–∂–¥–∞–µ—Ç, —á—Ç–æ –≤ —Å–∏–ª—É –º–≥–Ω–æ–≤–µ–Ω–Ω–æ—Å—Ç–∏ –º–æ–∂–Ω–æ —Ä–∞—Å—Å–º–∞—Ç—Ä–∏–≤–∞—Ç—å –∑–∞—Ä—è–¥–∫—É –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–∞ –∫–∞–∫ —Ç—É–Ω–Ω–µ–ª–∏—Ä–æ–≤–∞–Ω–∏–µ —ç–ª–µ–∫—Ç—Ä–æ–Ω–æ–≤ —á–µ—Ä–µ–∑ –∫–ª—é—á, –≤ –ø—Ä–æ—Ü–µ—Å—Å–µ –∫–æ—Ç–æ—Ä–æ–≥–æ —ç–Ω–µ—Ä–≥–∏—è –∏ —Ç–µ—Ä—è–µ—Ç—Å—è. –í—ã—Ö–æ–¥–∏—Ç, —á—Ç–æ –¥–ª—è —Ä–∞–∑—Ä–µ—à–µ–Ω–∏—è –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä–Ω—ã—Ö –ø–∞—Ä–∞–¥–æ–∫—Å–æ–≤ –¥–æ–±–∞–≤–ª—è—Ç—å –∏–Ω–¥—É–∫—Ç–∏–≤–Ω–æ—Å—Ç–∏ –∏–ª–∏ —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏—è –≤ —Å—Ö–µ–º—É –Ω–µ –æ–±—è–∑–∞—Ç–µ–ª—å–Ω–æ.
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
kentgaryk

|
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: –ù–∏–∫–∞–∫ –Ω–µ –º–æ–≥—É –≤—ä–µ—Ö–∞—Ç—å –≤ —Å–∞–º—ã–µ —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã–µ –≤–æ–ø—Ä–æ—Å—ã.  –î–æ–±–∞–≤–ª–µ–Ω–æ: –î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± —è–Ω–≤ 23, 2021 04:02:49 |
|
| –î—Ä—É–≥ –ö–æ—Ç–∞ |
 |
–ö–∞—Ä–º–∞: 127
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 11154
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä —è–Ω–≤ 08, 2014 04:21:09
–°–æ–æ–±—â–µ–Ω–∏–π: 32325
–û—Ç–∫—É–¥–∞: –ú–æ—Å–∫–≤–∞
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
|
lumped.net –ø–∏—Å–∞–ª(–∞): –ö—É–¥–∞ —É—à–ª–∞ –¥—Ä—É–≥–∞—è –ø–æ–ª–æ–≤–∏–Ω–∞ —ç–Ω–µ—Ä–≥–∏–∏? - –≤—ã—Ö–æ–¥–∏—Ç —á—Ç–æ –≤ –∫–ª—é—á, –ø–æ—Å–∫–æ–ª—å–∫—É –Ω–∏–∫–∞–∫–∏—Ö –¥—Ä—É–≥–∏—Ö —ç–ª–µ–º–µ–Ω—Ç–æ–≤ –≤ —Å—Ö–µ–º–µ –Ω–µ—Ç. –ü–∞—Ä–∞–¥–æ–∫—Å –ø—Ä–µ–æ–¥–æ–ª—ë–Ω (—à—É—Ç–∫–∞). –¢–æ–∂–µ –º–Ω–µ –ø–∞—Ä–∞–¥–æ–∫—Å. –≠—Ç–∏ –∑–∞–¥–∞—á–∫–∏ –º—É—Å–æ–ª–∏–ª–∏ –Ω–∞ —à–∫–æ–ª—å–Ω—ã—Ö –æ–ª–∏–º–ø–∏–∞–¥–∞—Ö –µ—â–µ 40-50 –ª–µ—Ç –Ω–∞–∑–∞–¥, –∑–∞—Ä—è–∂–∞—è –æ–¥–∏–Ω –∏–¥–µ–∞–ª—å–Ω—ã–π –∫–æ–Ω–¥–µ–Ω—Å–∞—Ç–æ—Ä –æ—Ç –¥—Ä—É–≥–æ–≥–æ. –ï—Å–ª–∏ —ç–ª–µ–º–µ–Ω—Ç—ã –∏–¥–µ–∞–ª—å–Ω—ã —Ç–æ –≤ —Ü–µ–ø–∏ –≤–æ–∑–Ω–∏–∫–∞–µ—Ç –±–µ—Å–∫–æ–Ω–µ—á–Ω—ã–π —Ç–æ–∫, –∫–æ—Ç–æ—Ä—ã–π –Ω–∞ –Ω—É–ª–µ–≤–æ–º —Å–æ–ø—Ä–æ—Ç–∏–≤–ª–µ–Ω–∏–∏ —Ü–µ–ø–∏ –¥–∞–µ—Ç –∫–æ–Ω–µ—á–Ω—ã–µ –ø–æ—Ç–µ—Ä–∏ —ç–Ω–µ—Ä–≥–∏–∏ –ø–æ –∑–∞–∫–æ–Ω—É –î–∂–æ—É–ª—è-–õ–µ–Ω—Ü–∞ . –ê –µ—Å–ª–∏ —ç–ª–µ–º–µ–Ω—Ç—ã –Ω–µ –∏–¥–µ–∞–ª—å–Ω—ã —Ç–æ –≤–æ–æ–±—â–µ –≤—Å–µ –æ—á–µ–≤–∏–¥–Ω–æ. –°–ø–æ–π–ª–µ—Ä
|
|
| –í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö |
|
 |
 
|
–°—Ç—Ä–∞–Ω–∏—Ü–∞ 170 –∏–∑ 180
|
[ –°–æ–æ–±—â–µ–Ω–∏–π: 3585 ] |
... , , , , , , ... |
–ö—Ç–æ —Å–µ–π—á–∞—Å –Ω–∞ —Ñ–æ—Ä—É–º–µ |
–°–µ–π—á–∞—Å —ç—Ç–æ—Ç —Ñ–æ—Ä—É–º –ø—Ä–æ—Å–º–∞—Ç—Ä–∏–≤–∞—é—Ç: –Ω–µ—Ç –∑–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω–Ω—ã—Ö –ø–æ–ª—å–∑–æ–≤–∞—Ç–µ–ª–µ–π –∏ –≥–æ—Å—Ç–∏: 14 |
|
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –Ω–∞—á–∏–Ω–∞—Ç—å —Ç–µ–º—ã
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –æ—Ç–≤–µ—á–∞—Ç—å –Ω–∞ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ —Ä–µ–¥–∞–∫—Ç–∏—Ä–æ–≤–∞—Ç—å —Å–≤–æ–∏ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ —É–¥–∞–ª—è—Ç—å —Å–≤–æ–∏ —Å–æ–æ–±—â–µ–Ω–∏—è
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –¥–æ–±–∞–≤–ª—è—Ç—å –≤–ª–æ–∂–µ–Ω–∏—è
|
|
|





































